Image Matching from Handcrafted to Deep Features A Survey¶

摘要¶

作为各种视觉应用中的一个基本且关键的任务，图像匹配可以从两个或更多图像中识别并对应相同或相似的结构/内容。在过去的几十年里，随着深度学习技术的发展，出现了越来越多种类和多样性的图像匹配方法。然而，关于针对不同场景和任务需求选择哪种方法以及如何设计更精确、稳健和高效的图像匹配方法仍然存在一些问题。这激励我们进行了一项全面而系统的综述和分析，涵盖了经典和最新的技术。遵循基于特征的图像匹配流程，我们首先介绍了特征检测、描述和匹配技术，从手工制作的方法到可训练的方法，并对这些方法在理论和实践中的发展进行了分析。其次，我们简要介绍了几种典型的基于图像匹配的应用，以全面了解图像匹配的重要性。此外，我们还通过在代表性数据集上进行广泛实验，对这些经典和最新的技术进行了全面和客观的比较。最后，我们总结了图像匹配技术的当前状态，并提供了关于未来工作的深刻讨论和展望。这项综述可以作为图像匹配和相关领域的研究人员和工程师的参考资料。

1 引言¶

在全球自动化和人工智能时代，广泛应用于引导机器感知和理解环境以进行更好的决策的基于视觉的人工系统扮演着重要角色。然而，在特定需求下如何处理感知信息，以及如何理解多个视觉目标之间的差异和/或关系，是各个领域的关键主题，包括计算机视觉、模式识别、图像分析、安全和遥感等。作为这些复杂任务中的一个关键而基本的问题，图像匹配，也被称为图像注册或对应，旨在识别并对应来自两个或更多图像的相同或相似的结构/内容。这项技术用于高维结构恢复以及信息识别和集成，如三维重建、视觉同时定位和地图构建（VSLAM）、图像拼接、图像融合、图像检索、目标识别和跟踪，以及变化检测等。

图像匹配在配对两个对象方面具有丰富的含义，因此派生出许多具体任务，例如稀疏特征匹配、密集匹配（如图像注册和立体匹配）、块匹配（检索）、二维和三维点集注册以及图匹配。一般而言，图像匹配由匹配特征的性质和匹配策略两部分组成，这表明了用于匹配以及如何匹配它们的方法。最终的目标是将感知到的图像几何变换到参考图像的共同空间坐标系统中，并将它们的公共区域像素到像素对齐（即图像注册）。为此，有一种直接策略，也称为基于区域的方法，通过在预定义大小的滑动窗口或甚至整个图像中使用原始图像像素强度或像素域变换后的信息的相似性测量来注册两个图像，而无需尝试检测任何显著的图像结构。

另一个经典且广泛采用的流程称为基于特征的方法，即特征检测和描述、特征匹配、变换模型估计、图像重采样和变换，已经在著名的综述论文中引入（Zitova and Flusser 2003），并应用于各个领域。基于特征的图像匹配因其灵活性和稳健性以及广泛应用的能力而受欢迎。特别是，特征检测可以从图像中提取出独特的结构，特征描述可以被视为广泛用于图像编码和相似性测量的图像表示方法，如图像分类和检索。此外，由于在深度特征获取和非线性表达方面的强大能力，应用深度学习技术进行图像信息表示和/或相似性测量以及图像对变换的参数回归是当前图像匹配领域的热门话题，与传统方法相比，已经证明可以获得更好的匹配性能并具有更大的潜力。

在现实世界的环境中，用于匹配的图像通常来自相同或相似的场景/对象，但在不同的时间、不同的视点或不同的成像模式下捕获。特别是，希望建立正确的对应关系需要一种稳健且高效的匹配策略，因此刺激了各种方法的发展，以实现更好的效率、稳健性和准确性。尽管在几十年的时间里已经设计出了大量的技术，但在以下几个方面仍然存在统一框架的挑战性任务：

• 直接匹配图像的基于区域的方法通常依赖于适当的块相似性测量，用于在图像之间创建像素级匹配。它们可能会消耗大量计算资源，并对图像畸变、噪声引起的外观变化、不同的光照和不同的成像传感器敏感，这可能会对相似性测量和匹配搜索产生负面影响。因此，通常这些方法只能在小的旋转、缩放和局部变形下工作良好。
• 基于特征匹配方法通常更高效，并且可以更好地处理几何变形。但它们是基于显著特征检测和描述、特征匹配和几何模型估计的，这也可能具有挑战性。一方面，在基于特征的图像匹配中，很难定义和提取属于现实世界中相同位置的高比例和大数量的特征，以确保匹配性。另一方面，将 \(N\) 个特征点与在另一幅图像中检测到的 \(N\) 个特征点匹配会创建总共 \(N!\) 可能的匹配，通常从高分辨率图像中提取出数千个特征，并且主导的离群值和噪声通常包含在点集中，这对现有的匹配方法构成了重大困难。尽管已经提出了各种局部描述符，并将其与检测到的特征配对以简化匹配过程，但使用局部外观信息将不可避免地导致模糊和大量的虚假匹配，特别是对于质量较差、内容重复的图像以及经历严重的非刚性变形和极端视角变化的图像。
• 通常需要预定义的变换模型来指示两个图像或点集之间的几何关系。但它可能因不同的数据而异，在事先未知的情况下难以建模。对于涉及地面表面波动和图像视点变化引起的非刚性变换、具有不同运动特性的多个目标以及局部失真的图像对，简单的参数模型通常是不足够的。
• 深度学习的出现提供了一种新的方式，并显示出在解决图像匹配问题方面具有巨大潜力。然而，它仍然面临一些挑战。当应用于宽基线图像立体或在复杂和严重变形下进行注册时，从图像学习直接进行注册或变换模型估计的选择有限。将卷积神经网络（CNNs）应用于稀疏点数据以进行匹配、注册和图像对变换的参数回归也很困难，因为要匹配的点被称为非结构化或非欧几里德数据，因为它们的无序和分散的性质使得难以使用深度卷积技术操作和提取两个或多个点之间的空间关系（例如，相邻元素、相对位置以及多点之间的长度和角度信息）。

现有的综述侧重于图像匹配任务的不同部分，并未涵盖过去十年的文献。例如，早期的综述（Zitova and Flusser 2003; Tuytelaars and Mikolajczyk 2008; Strecha et al. 2008; Aanæs et al. 2012; Heinly et al. 2012; Awrangjeb et al. 2012;Lietal.2015）通常侧重于手工制作的方法，这对于研究基于 CNN 的方法并不足够。最近的综述涉及到可训练的技术，但它们通常只覆盖图像匹配领域的某个部分，要么关注检测器（Huang et al. 2018; Lenc and Vedaldi 2014），要么关注描述符（Balntas et al. 2017; Schonberger et al. 2017），要么关注特定的匹配任务（Ferrante and Paragios 2017; Haskins et al. 2020; Yan et al. 2016b; Maiseli et al. 2017），而其他综述则更多地关注相关应用（Fan et al. 2019; Guo et al. 2016; Zheng et al. 2018; Piasco et al. 2018）。 在这项综述中，我们的目标是提供关于现有图像匹配方法的最新和全面的摘要和评估，尤其是针对最近引入的基于学习的方法。更重要的是，我们对主流方法进行了详细的评估和分析，而这在现有文献中尚未涵盖。

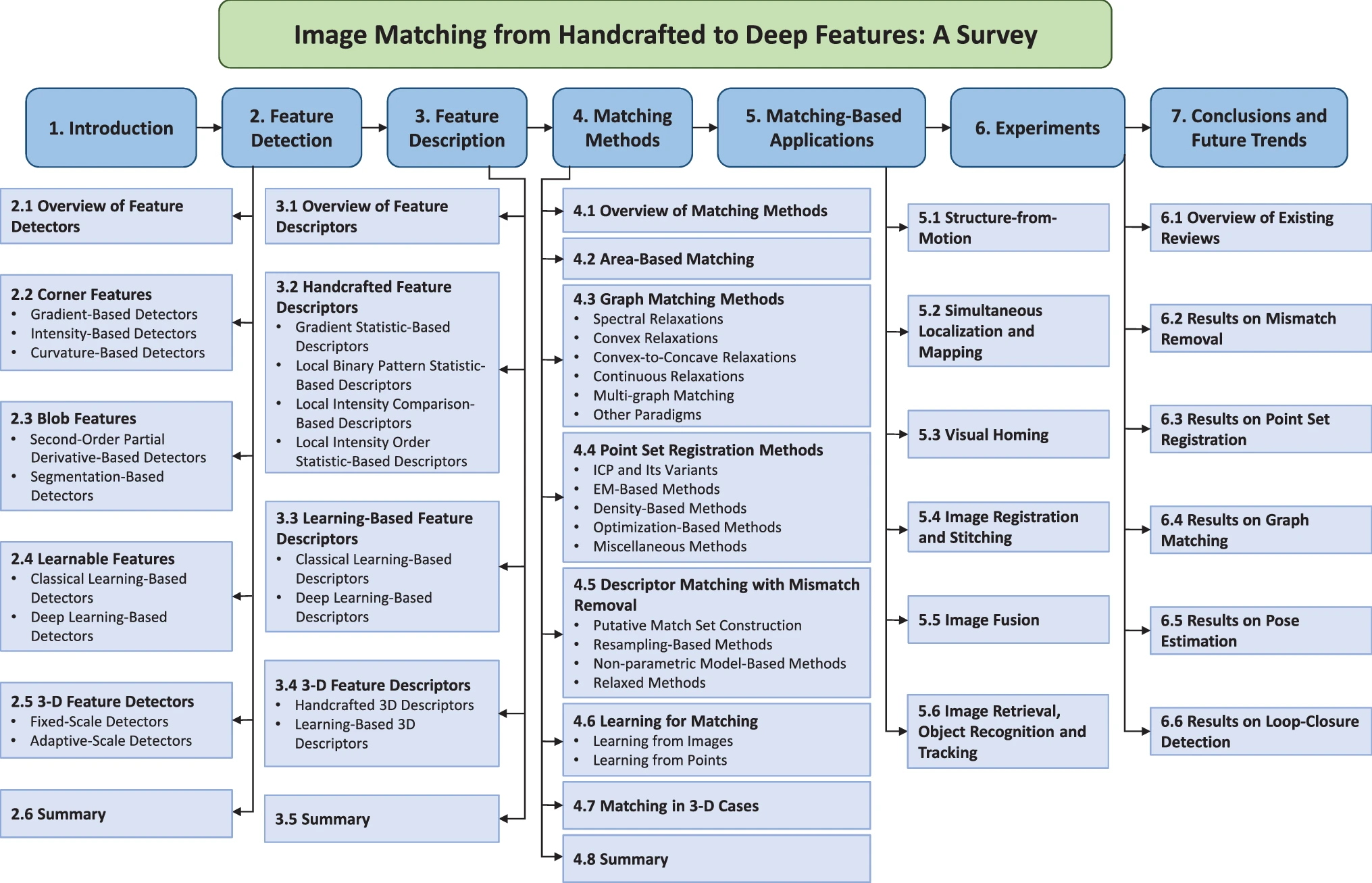
尽管还回顾了块匹配、点集匹配以及其他相关匹配任务，但此综述主要关注基于特征的匹配。总体组织如图 1 所示；第 2 和第 3 节分别描述了特征检测和描述技术，从手工制作的方法到可训练的方法。块匹配被分类为特征描述领域，并且还回顾了三维点集特征。在第 4 节中，我们介绍了不同的匹配方法，包括基于区域的图像匹配、纯点集注册、图像描述符相似性匹配和误匹配去除、图匹配以及基于学习的方法。第 5 节和第 6 节分别介绍了基于图像匹配的视觉应用和评估度量，包括性能比较。在第 7 节中，我们总结并讨论了可能的未来发展。

2 特征检测¶

早期的图像特征是手动注释的，仍然在一些低质量的图像匹配中使用。随着计算机视觉的发展和对自动匹配方法的需求，许多特征检测方法已经被引入，用于从图像中提取稳定和独特的特征。

2.1 特征检测概述¶

检测到的特征代表图像或现实世界中的特定语义结构，可以分为角点特征（Moravec 1977; Harris 等人 1988; Smith 和 Brady 1997; Rosten 和 Drummond 2006; Rublee 等人 2011），斑点特征（Lowe 2004; Bay 等人 2006; Agrawal 等人 2008; Yi 等人 2016），线条/边缘（Harris 等人 1988; Smith 和 Brady 1997; Canny 1987; Perona 和 Malik 1990），以及形态区域特征（Matas 等人 2004; Mikolajczyk 等人 2005）。然而，用于匹配的最流行特征是点（也称为关键点或兴趣点）。与线和区域特征相比，点易于提取，并且具有简化的形式，大致可以分为角点和斑点。 良好的兴趣点必须易于查找，并且理想情况下计算速度快，因为位于良好位置的兴趣点对于进一步的特征描述和匹配至关重要。为了提高（i）可匹配性，（ii）用于后续应用的能力，以及（iii）匹配效率和减少存储要求，已经提出了许多可靠的特征提取属性（Zitova 和 Flusser 2003; Tuytelaars 和 Mikolajczyk 2008），包括可重复性、不变性、稳健性和效率。特征检测的共同思想是构建一个特征响应以区分显着的点、线和区域，以及平坦和不明显的图像区域。这个想法随后可以被分类为基于梯度、强度、二阶导数、轮廓曲率、区域分割和基于学习的检测器。接下来，我们将对这些方法提供全面的特征检测介绍，重点关注基于学习的方法，以指导研究人员了解传统和可训练的检测器的工作方式，并提供其优点和缺点的见解。

2.2 角点特征¶

角点特征可以被定义为“L”，“T”，“X”形状的两条直线相交点，或者是轮廓的高曲率点。角点检测的常见思想是计算角点响应并将其与边缘、平坦或其他不太显著的图像区域区分开。传统的角点搜索可以使用不同的策略，即基于梯度、强度和轮廓曲率。可参考 Zitova and Flusser (2003), Li et al. (2015), Tuytelaars 和 Mikolajczyk (2008) and Rosten et al. (2010)

2.2.1 基于梯度的检测器¶

基于梯度的角点响应更倾向于使用图像的一阶信息来区分角点特征。最早的自动角点检测方法可以追溯到 Moravec 检测器（Moravec 1977），它首次引入了“兴趣点”的概念来定义独特的特征点，这些特征点是基于局部强度的自相关提取的。该方法计算并搜索每个像素在八个方向上的位移窗口中的最小强度变化，并且如果最小值优于给定的阈值，则检测到兴趣点。

然而，由于不连续的比较方向和尺寸，Moravec 检测器对方向或图像旋转不具有不变性。著名的 Harris 角点检测器（Harris 等人 1988）引入了解决各向异性和计算复杂性问题的方法。Harris 方法的目标是使用二阶矩阵或自相关矩阵找到最快和最低灰度值变化的方向，因此对方向和光照具有不变性，并且具有可靠的可重复性和独特性。Harris 在 Shi 和 Tomasi（1993）中进一步改进，通过使特征更加“分散”并更准确地定位来提高跟踪性能。

2.2.2 基于强度的检测器¶

通过将周围像素的强度与中心像素的强度进行比较，可以提出基于模板或强度比较的角点检测器，从而简化图像梯度计算。由于它们具有二进制的特性，因此它们在许多现代应用中广泛使用，特别是一些具有存储和实时要求的应用。

基于强度的角点检测器，即最小唯一值段吸收核（SUSAN）（Smith 和 Brady 1997），基于局部半径区域像素和核的亮度相似性。SUSAN 可以迅速实现，因为它不需要梯度计算。已经提出了许多类似的方法，这些方法基于亮度比较的概念，其中最著名的是 FAST 检测器（Trajković和 Hedley 1998）。FAST 使用与中心像素沿圆形模式的每个像素的二进制比较，然后使用机器学习（即 ID3 树 Quinlan 1986）策略确定更可靠的角点特征，该策略经过大量类似场景图像的训练，可以生成最佳的角点选择标准。

作为 SUSAN 的改进，FAST 具有极高的可重复性和广泛使用。为了提高 FAST 的效率而不损失效果，引入了 FAST-ER（Rosten 等人 2010），通过基于核周围进一步像素强度比较来增强可重复性。另一种改进是 AGAST（Mair 等人 2010），其中定义了另外两个像素亮度比较标准，然后在扩展配置空间中对其进行了优化和专门的决策树训练，从而使 FAST 检测器更通用和自适应。为了将 FAST 的效率与 Harris 检测器的可靠性相结合，Rublee 等人（2011）提出了一种集成的特征检测器和描述符，用于匹配，称为 ORB。ORB 使用 Harris 响应来选择一定数量的 FAST 角点作为最终检测到的特征。局部块的灰度质心和中心像素本身形成一个矢量，用于表示 ORB 特征的主方向，有助于计算 ORB 中的二进制描述符的相似性。最近，引入了一种类似于 Sadder 的检测器（Aldana-Iuit 等人 2016）来提取兴趣点。在此检测器中，通过对具有一定几何约束的两个同心圆上的强度比较来有效验证鞍点条件。与传统方法以及现代可训练方法（Komorowski 等人 2018）相比，Sadder 检测器可以实现更高的可重复性和更广泛的分布。

2.2.3 基于曲率的检测器¶

角点特征提取的另一种策略是基于检测到的高级图像结构，例如边缘、轮廓和显著区域。角点特征可以立即被定义为来自边缘或轮廓的中点/端点或稀疏采样（Belongie 等人 2002）。这些随后用于形状匹配或点注册，特别是对于纹理较少或二进制类型的图像对。基于曲率策略旨在根据检测到的图像曲线状边缘来提取具有最大曲率的角点，这一策略从边缘提取和选择方法开始，然后两个后续步骤是曲线平滑和曲率估计。角点最终通过选择曲率极值点来确定。通常，在轮廓曲率角点检测中，首先需要边缘检测器。

在曲线平滑中，由于曲线点的量化位置，斜率和曲率难以评估。曲线中的噪声和局部变形也可能对特征的稳定性和独特性产生严重影响。因此，在曲率计算之前或期间应该实施平滑方法，以使曲率极值点与其他曲线点更为明显。通常使用两种平滑策略，即直接和间接方法。直接平滑，例如高斯平滑（Mokhtarian 和 Suomela 1998; Pinheiro 和 Ghanbari 2010），消除了噪声，并可能在一定程度上改变曲线位置。相比之下，间接平滑策略，例如区域支持方法或基于弦长的方法（Ramer 1972; Awrangjeb 和 Lu 2008），可以保留曲线点位置。

至于曲率估计，对于平滑曲线的每个点，需要一个用于角点搜索的显著响应测量，即曲率。曲率估计方法通常分为直接和间接两类。前者基于代数或几何估计，例如余弦、局部曲率和切线偏转（Mokhtarian 和 Suomela 1998; Rosenfeld 和 Weszka 1975; Pinheiro 和 Ghanbari 2010）。后者以间接方式估计曲率，通常用作显著性测量，例如通过曲线上的几个移动矩形计数曲线点（Masood 和 Sarfraz 2007），使用从连接曲线两个端点的弦到曲线点的垂直距离（Ramer 1972），以及其他替代方法（Zhang 等人 2010, 2015）。与间接估计方法相比，直接方法对噪声和局部变化更敏感，因为它们考虑了较少的邻近点。

最后，可以使用阈值策略确定角点，以消除虚假和不明显的点（Mokhtarian 和 Suomela 1998; Awrangjeb 和 Lu 2008）。可以从轮廓曲率角点调查中获取更多详细信息（Awrangjeb 等人 2012）。此外，最近引入了一种名为 MSFD（Mustafa 等人 2018）的多尺度分割型角点检测器，用于宽基线场景匹配和重构。MSFD 中的特征点是通过使用现成的分割方法在三个或更多区域的边界相交处检测的。MSFD 可以为宽基线图像匹配生成丰富且准确的角点特征，并具有高重建性能。

上述角点特征检测器容易位于图像的轮廓或边缘结构中（即分布不分散或不均匀），并受到两个图像之间的尺度和仿射变换的限制。在三种类型的角点检测策略中，基于梯度的方法能够更精确地定位，而基于强度的方法在效率方面具有优势。基于曲率方法需要更多的计算，但它们对于处理无纹理或二进制图像（例如红外和医学图像）等图像更为合适，因为这些类型的图像无法用于基于图像线索的特征描述符，而点描述符通常与匹配任务（即点集注册或形状匹配）耦合。有关详细信息，请参阅第 3 和第 4 节。

2.3 斑点特征¶

斑点特征通常被定义为局部封闭区域（例如，具有圆形或椭圆形的规则形状），在这个区域内的像素被认为彼此相似，并且与周围区域有所不同。斑点特征可以用以下形式表示 \((x, y, \theta)\) ，其中 \((x, y)\) 表示特征位置的像素坐标，\(\theta\) 表示特征的形状信息，包括尺度和/或仿射变换信息。在过去几十年里，已经引入了许多斑点特征检测方法，它们大致可以分为二阶偏导数和区域分割两种类型的检测器。基于二阶偏导数的方法基于仿射不变的拉普拉斯尺度选择和/或 Hessian 矩阵计算。而基于分割的方法更倾向先通过分割形态区域来检测斑点特征，然后通过椭圆拟合来估计仿射信息。与角点特征相比，斑点特征对于精度要求较高的视觉应用更有用，因为有更多的图像线索用于特征识别和表示，从而使斑点特征对图像变换更加准确和鲁棒。

2.3.1 基于二阶偏导数的检测器¶

在基于二阶偏导数的方法中，根据尺度空间理论，使用了高斯拉普拉斯（LoG）（Lindeberg 1998）。在这里，首先使用拉普拉斯算子进行边缘检测，根据图像的二阶导数的零交叉点进行操作，然后应用高斯卷积滤波作为预处理步骤，以减少噪声。

LoG 可以检测到具有归一化响应的局部极值点和区域，这些响应来自于高斯核的圆对称性。不同标准差的高斯函数可以检测不同尺度上的尺度不变斑点，通过在多尺度空间中搜索极值来得到最终稳定的斑点特征。差分高斯（DoG）（Lowe et al. 1999; Lowe 2004）滤波器可以用来近似 LoG 滤波器，并大大加快计算速度。另一种经典的斑点特征检测策略是基于 Hessian 矩阵行列式（DoH）（Mikolajczyk and Schmid 2001, 2004）。这种方法更具仿射不变性，因为可以应用第二矩阵的特征值和特征向量来估计和校正仿射区域。

最近的视觉应用广泛使用 DoG、DoH 或两者结合的兴趣点检测。著名的 SIFT（Lowe et al. 1999; Lowe 2004）在 DoG 金字塔中提取关键点，然后使用局部强度值的 Hessian 矩阵进行滤波（相关描述部分将在下一节中进行介绍）。Mikolajczyk 等人将 Harris 和 Hessian 检测器与 Laplacian 和 Hessian 矩阵结合，用于尺度和仿射特征检测（Mikolajczyk and Schmid 2001, 2004），即 Harris/Hessian-Laplacian/仿射。SURF（Bay et al. 2006）通过使用 Haar 小波计算来近似基于 Hessian 矩阵的检测器，再加上积分图像策略，从而简化了二阶微分模板的构建，得以对 SIFT 进行加速。

已经连续提出了一些基于 SIFT 和 SURF 的改进方法，以在后续应用中具有更好的性能。这些改进包括全仿射不变的 SIFT 检测器（ASIFT）（Morel and Yu 2009），一种使用双边滤波近似 Laplace 计算的中心周围极值策略特征检测器，以提高效率，以及在 DARTs（Marimon et al. 2010）中使用分段三角形滤波器高效近似 DoH。此外，SIFT-ER 检测器（Mainali et al. 2013）使用余弦调制的高斯滤波器，以获得具有最小尺度空间定位误差的高特征可检测性，其中滤波器系统具有高度精确的滤波器近似，无需任何图像下/上采样。还引入了一种基于边缘焦点的斑点检测器（Zitnick and Ramnath 2011）用于匹配任务。在这个检测器中，边缘焦点被定义为图像中距离最近的边缘大致等距的点，边缘的方向垂直于此点。

与圆形的高斯响应函数不同，KAZA 检测器采用非线性偏扩散滤波来搜索斑点特征（Alcantarilla et al. 2012）。通过在金字塔框架中嵌入快速显式扩散，实现了加速版本 AKAZA（Alcantarilla and Solutions 2011），极大地加速了非线性尺度空间中的特征检测。然而，它仍然受到计算复杂性的限制。另一种方法是 WADE（Salti et al. 2013），它通过波传播函数实现非线性特征检测。

2.3.2 基于分割的检测器¶

基于分割的斑点检测器首先基于像素强度或零梯度进行不规则区域分割。其中最著名的基于区域分割的斑点特征是极大稳定极值区域（MSER）（Matas et al. 2004）。它提取在大范围强度阈值下保持稳定的区域。这种方法不需要额外的处理来估计尺度，对大的视角变化具有鲁棒性。术语“最大稳定”描述了阈值选择过程，因为每个极值区域都是通过阈值分割图像的分水岭图像的连通组成部分。在 Kimmel 等人（2011）中引入了 MSER 的扩展方法，以利用形状结构线索。其他改进是基于主曲率图像的分水岭区域（Deng et al. 2007; Ferraz and Binefa 2012）或考虑颜色信息以提高区分度（Forssén 2007）。

与 MSER 类似，其他基于分割的特征，如基于强度和边缘的区域（Tuytelaars and Van Gool 2004），也用于仿射协变区域检测。然而，这种类型的特征检测对于特征匹配的用途不太有用，逐渐发展成为计算机视觉中的显著性检测和分割。关于特定方法的详细研究和综合评论可以在 Mikolajczyk 等人（2005）和 Li 等人（2015）中找到。

2.4 可学习特征¶

近年来，数据驱动的学习方法在通用视觉模式识别任务中取得了重大进展，并已应用于图像特征检测。这个流程可以大致分为经典学习和深度学习两种方式。

2.4.1 经典学习方法¶

早在过去十年中，经典的学习方法，如决策树、支持向量机（SVM）和其他与深度学习相对立的分类器，已经在手工制作的关键点检测中使用（Trajkovi ́ c and Hedley 1998; Strecha et al. 2009; Hartmann et al. 2014; Richardson and Olson 2013）。FAST（Trajkovi ́ c and Hedley 1998）检测器是首次尝试使用传统学习方法进行可靠的可匹配点识别的尝试，类似的策略已经应用在许多后续改进中（Mair et al. 2010; Rublee et al. 2011）。Strecha 等人（2009）训练了 Wald-Boost 分类器，以在预对齐的训练集上学习高可重复性的关键点。

最近，Hartmann 等人（2014）表明可以从结构-运动（SfM）管道中学习，以预测哪些候选点是可匹配的，从而显著减少了兴趣点的数量而不会失去过多的真实匹配。同时，Richardson 和 Olson（2013）报告说，可以通过在卷积滤波器空间中进行随机采样来学习手工设计的检测器，并尝试通过频域约束的学习策略来找到最佳的滤波器。然而，经典学习仅用于通过分类器学习可靠的特征选择，而不是直接从原始图像中提取兴趣特征，直到深度学习的出现。

2.4.2 基于深度学习的检测器¶

受到手工特征检测器的启发，基于 CNN 的检测的一般解决方案是构建响应图，以在监督（Yi 等人 2016; Verdie 等人 2015; Zhang 等人 2017b）、自监督（Zhang 和 Rusinkiewicz2018; DeTone 等人 2018）或无监督方式（Lenc 和 Vedaldi2016; Savinov 等人 2017; Ono 等人 2018; Georgakis 等人 2018; Barroso-Laguna 等人 2019）中搜索兴趣点。任务通常转化为一个回归问题，可以在变换和成像条件不变性约束下以可微分的方式进行训练。监督方法已经显示出使用锚点（例如从 SIFT 方法获取的锚点）来指导它们的训练的好处，但是由于锚点本身在接近区域内本质上难以合理定义，可能会受限于锚点构建方法的性能，因为如果在附近没有锚点存在，网络可能会阻止提出新的关键点（Barroso-Laguna 等人 2019）。自监督和无监督方法训练检测器时不需要任何人工标注，只需要两幅图像之间的几何约束来进行优化指导；有时需要简单人工帮助进行预训练（DeTone 等人 2018）。此外，许多方法通过与特征描述和匹配的联合训练将特征检测集成到整个匹配管道中（Yi 等人 2016; DeTone 等人 2018; Ono 等人 2018; Shen 等人 2019; Dusmanu 等人 2019;Choyetal.2016; Rocco 等人 2018; Dusmanu 等人 2019; Revaud 等人 2019），这可以增强最终的匹配性能并以端到端的方式优化整个过程。

例如，TILDE（Verdie 等人 2015）训练多个分段线性回归模型以检测在天气和照明条件大幅变化的情况下可重复使用的关键点。首先，它使用 DoG 进行训练集收集，从相同视点拍摄的多个训练图像中识别出良好的关键点候选项，然后训练一个通用的回归器来预测一个得分图，其经过非极大值抑制（NMS）后的最大值可以视为所需的兴趣点。

DetNet（Lenc 和 Vedaldi 2016）是学习局部协变特征的第一个完全通用的公式；它将检测任务构建为一个回归问题，然后导出一个协方差约束条件，以在几何变换下自动学习本地特征检测的稳定锚点。与此同时，Quad-net（Savinov 等人 2017）通过单一的实值响应函数实现了在变换不变的分位数排名下的关键点检测，使其能够通过优化可重复排名来完全从头开始学习检测器。在 Zhang 和 Rusinkiewicz（2018）中，类似的检测器将这种“排名”损失与“峰度”损失相结合，产生了一个更具可重复性的检测器。

Zhang 等人（2017b）定义“标准块”和“规范特征”这两个新概念，基于此定义了新公式，提出了 TCDET 检测器，以便平等关注区分性和协变约束。所提出的检测器可以在各种图像变换下检测出具有区分性和可重复性的特征。Key.Net（BarrosoLaguna 等人 2019）在浅层多尺度架构中结合了手工制作和学习的 CNN 滤波器，提出了一种轻量/高效的可训练检测器。手工制作的滤波器提供了本地化、评分和排名可重复特征的锚点结构，这些特征被馈送到学习的滤波器中。CNN 用于表示不同级别的尺度空间，损失函数被定义为从不同尺度检测出强健的特征点，并最大化可重复性得分。在 Mishkin 等人（2017, 2018）中，也使用 CNN 学习了基于仿射区域的兴趣点。

将检测器整合到匹配流水线中的方法与上面专门设计用于检测的方法类似。主要区别可能在于训练方式，核心挑战在于使整个过程可微分。例如，Yi 等人（2016）尝试基于输入的四个块共同训练检测器、方向估计器和描述符。他们提出的 LIFT 可以被视为 SIFT 的可训练版本，需要来自 SfM 系统的监督来确定特征锚点。训练过程是从描述符到检测器逐个进行的，可以使用学到的结果来指导检测器的训练，从而提高了可检测性。与 LIFT 不同，SuperPoint（DeTone 等人 2018）通过输入全尺寸图像引入了一个完全卷积模型，并在一个前向传递中联合计算像素级兴趣点位置和相关描述符；为了生成伪地面真值并进行预训练，构建了一个合成数据集，同时，通过自监督训练实现了它的同质性适应模块，从而提高了检测的可重复性。

LF-Net（Ono 等人 2018）将端到端流程限制在一个分支中，以可微分的方式优化整个过程；它还使用在全尺寸图像上操作的完全卷积网络生成丰富的特征评分图，然后可以用于提取关键点位置和特征属性，如尺度和方向；同时，它执行一种可微分的 NMS，即 softargmax，用于子像素定位，增加了关键点的准确性和显著性。与 LF-Net 类似，RF-Net（Shen 等人 2019）选择多尺度上的高响应像素作为关键点，但响应图是由感受野特征图构建的。Bhowmik 等人（2020）指出，这些低级匹配分数的提高不一定会转化为高级视觉任务的更好性能，因此他们将特征检测器嵌入到一个完整的视觉流水线中，其中可学习参数以端到端的方式训练。作者通过强化学习的原则克服了关键点选择和描述符匹配的离散性。Luo 等人（2020）提出了 ASFeat，以探索特征点的局部形状信息，并通过联合学习本地特征检测器和描述符来增强点检测的准确性。另一种与检测相关的基于学习的方法是估计方向（Moo Yi 等人 2016），而空间变换网络（STN）（Jaderberg 等人 2015）也可以是深度学习检测器在旋转不变性方面的重要参考（Yi 等人 2016；Ono 等人 2018）。

与本地特征描述符不同，对于最近的基于 CNN 的显著特征检测器，几乎没有相关综述。据我们所知，最近的一项调查（Lenc 和 Vedaldi 2014）侧重于本地特征检测。它介绍了从手工制作检测器到加速和学习检测器的几种知名方法的基本思想。

2.5 3D 特征检测器¶

专门用于 3D 关键点检测的，Tombari 等人（2013）提供了关于最新方法的详细评估和性能的出色综述。简言之，现有的方法被分为两类，固定尺度检测器和自适应尺度检测器。在这两类中，关键点被选择为预定义的显著性测量的局部极值点。区别在于尺度特征的参与，尺度特征定义了后续描述阶段的支持。固定尺度检测器倾向于在特定尺度级别搜索关键点，这是作为先验信息给出的。而自适应尺度检测器要么通过采用在表面上定义的尺度空间来扩展二维图像的尺度概念，要么通过将三维数据嵌入到二维平面上来实现传统的尺度空间分析。

2.5.1 固定尺度检测器¶

Chen 和 Bhanu（2007）引入了局部表面贴片（LSP）方法。在 LSP 中，点的显著性通过其形状指数（Dorai 和 Jain 1997）来测量，该形状指数由点处的主曲率定义。Zhong（2009）引入了内在形状签名（ISS）方法，其中显著性源自支持区域的散射矩阵的特征值分解。在这种方法中，使用特征值的比率来修剪一些点，最终显著性由特征向量确定。通过这种方式，可以识别出在每个主方向上变化很大的点。类似于 ISS，Mian 等人（2010）也利用散射矩阵来修剪不明显的点，但使用了不同的基于曲率的显著性测量。Sun 等人（2009）提出了基于形状热核的方法（HKS），基于形状上的热扩散过程的属性。在这种方法中，显著性测量是通过将热核限制到时间域来定义的。热核是由底层流形唯一确定的，这使得 HKS 成为形状的紧凑特征描述。

2.5.2 自适应尺度检测器¶

在检测中，自适应地适应尺度是理想的。为此，Unnikrishnan 和 Hebert（2008）提出了拉普拉斯-贝尔特拉米尺度空间，通过计算围绕每个点的增加支持上的设计函数来实现。这个函数由一个反映了底层形状的局部平均曲率的新颖运算符定义，并提供了显著性信息。Zaharescu 等人（2009）提出了 MeshDoG 方法，类似于 2D 情况下的 DoG 运算符（Lowe 2004）；不过，该运算符是在流形上定义的标量函数上计算的。DoG 运算符的输出代表了关键点检测的显著性。Castellani 等人（2008）也使用了 DoG 运算符在 3D 网格上直接构建尺度空间。Mian 等人（2010）提出了一种用于提取尺度不变特征的自动尺度选择技术。通过增加支持大小来构建尺度空间，并通过沿尺度进行的 NMS 来执行每个关键点的自动尺度选择。Bronstein 和 Kokkinos（2010）解决了 HKS 对尺度敏感的缺点，他们使用了傅立叶变换幅度来从 HKS 中提取尺度不变量，而无需执行尺度选择。Sipiran 和 Bustos（2011）将着名的 Harris 运算符（1988）扩展到 3D 数据，并使用自适应尺度确定技术。有关其他自适应尺度检测器的进一步讨论，请参阅 Tombari 等人（2013）。Salti 等人（2015）设计了一个基于学习的 3D 关键点检测器，其中关键点检测问题被视为一个二进制分类问题，以确定哪些支持可以由预定义的 3D 描述符正确匹配。

2.6 总结¶

特征检测器的基本思想是通过响应值区分感兴趣的特征与其他特征，从而解决了两个问题：（i）如何在图像中定义可辨别的模式，以及（ii）如何在不同的图像条件和图像质量下重复检测显著特征（Zhang 等人，2017b）。随着这些检测器的发展，主要的改进和常见的策略与四个方面相关，即特征响应类型和效率、鲁棒性和准确性的改进，这导致了检测到的特征的匹配性增加以及其后续应用性能的改善。

对于传统方法，使用更多的图像线索可以提高鲁棒性和可重复性，但通常需要更多的计算成本。除了使用低阶特征检测器之外，还设计了一些策略，如近似和预计算，以大大加速计算并保持可匹配性。为了确保鲁棒性，通常在搜索稳定特征时需要尺度和仿射信息估计。而对于准确性的增强，局部极值搜索以获得亚像素精度以及在像素和尺度空间中避免局部聚集的特征的非极大值抑制（NMS）策略是传统流程中的两个常见选择。

至于基于学习的检测器，可以基于由 CNN 捕获的，除强度、梯度或二阶导数之外的高级线索来提取可重复和显著的关键点。然而，效率很大程度上取决于网络结构，早期的深度学习方法通常需要大量时间。最近提出的方法，如 SuperPoint 和 Key.Net，已经在保持最先进性能的同时实现了实时处理。多尺度采样或改变感受野可以使这些基于深度学习的检测器对尺度具有不变性，其中尺度或旋转信息直接在网络中估计。它们可以取得良好的结果，因为深度学习技术可以轻松区分相同的结构，尽管图像受到明显的变化和几何变换的影响。准确性可以直接在学习方法的损失函数中进行优化，而 NMS 的可微分形式通常用于亚像素精度位置和可重复性的增强。

3 特征描述¶

一旦从原始图像中检测到具有辨别性的兴趣点，就需要为每个特征配对一个局部块描述符，以便在两个或更多图像之间正确且高效地建立特征对应关系。换句话说，特征描述符通常用于将感兴趣点周围的原始局部信息转换为稳定且具有辨别性的形式，通常以高维向量的形式存在，以便在描述符空间中两个对应的特征尽可能接近，而两个不对应的特征则尽可能远离。

3.1 特征描述符概述¶

特征描述的处理过程可以分为三个步骤：局部低级特征提取、空间池化和特征归一化（Lowe 2004；Rublee 等人 2011；Brown 等人 2010）。首先，必须提取局部图像区域的低级信息。这些信息包括像素强度和梯度，或者是从一系列可转向滤波器中获得的信息。随后，局部块被划分为若干部分，局部信息在每个部分中被池化，然后通过使用池化方法（例如矩形网格（Lowe 2004），极坐标网格（Mikolajczyk 和 Schmid 2005），高斯采样（Tola 等人 2010）以及其他方法（Rublee 等人 2011）将它们连接在一起。联合特征表示被转化为更具辨别性的表示形式，这可能以简化形式保留了重要信息，以提高匹配性能。最后，从汇总的局部信息的归一化结果中获得描述符，旨在将聚合的结果映射到浮点或二进制值的长向量中，以便轻松评估图像特征之间的相似性。与特征检测器类似，现有的描述符被提出和改进，以实现高度的鲁棒性、高效性和辨别性，以解决图像匹配问题。在特征描述和匹配任务中，正确估计裁剪图像块的大小和方向是核心问题。通过正确识别大小和方向，匹配方法可以对全局和/或局部的变形（如旋转和缩放）具有鲁棒性和不变性。特征描述的原始目的是通过与使用原始图像信息的直接相似度测量相比，集中在辨别性增强上。许多精心设计的描述符可以通过使用池化参数优化、采样规则设计或使用机器学习和深度学习技术来提高辨别性和匹配性能。特征描述引起了越来越多的关注。描述符可以被看作是给定图像的可区分和鲁棒的表示形式，它们广泛应用于图像匹配以及基于图像相似度测量的图像检索、人脸识别和其他任务中。然而，使用原始图像信息对两个图像块进行直接相似度测量将被视为一种基于区域的图像匹配方法，将在下一节中进行介绍。至于基于图像块的特征描述符，我们将根据其数据类型，审查传统的浮点和二进制描述符。新的子节将添加到最近的数据驱动方法中，包括经典的机器学习和新兴的基于深度学习的方法。我们将全面审查手工制作和基于学习的特征描述方法，并展示这些方法之间的联系，为读者提供有关进一步研究的有用指导，特别是使用深度学习/CNN 技术开发更好的描述方法。此外，我们还将审查 3D 特征描述符，其中特征通常是从点数据中获得的，而不包含任何图像像素信息，但具有空间位置关系（例如，3D 点云配准）。

3.2 手工制作的特征描述符¶

手工制作的特征描述符通常依赖于专家的先验知识，它们在许多视觉应用中仍然广泛使用。遵循传统局部描述符的构建过程，第一步是提取低级信息，可以简要分类为图像梯度和强度。随后，应用常用的池化和归一化策略，例如统计和比较，以生成长且简单的矢量，以便根据数据类型（浮点或二进制）进行区分性描述。因此，手工制作的描述符大多依赖于其作者的知识，描述策略可以分为梯度统计、局部二值模式统计、局部强度比较和局部强度顺序统计等几种。

3.2.1 基于梯度统计的描述符¶

梯度统计方法通常用于生成浮点型描述符，如梯度直方图（HOG）（Dalal 和 Triggs 2005），它在 SIFT（Lowe 等人 1999；Lowe2004）中被引入，并且其改进版本（Bay 等人 2006；Morel 和 Yu 2009；Dong 和 Soatto 2015；Tola 等人 2010）仍然广泛应用于一些现代视觉任务中。在 SIFT 中，特征的尺度和方向分别由 DoG 计算和从检测到的关键点周围的局部圆形区域中梯度方向直方图中的最大箱决定，从而实现了尺度和旋转不变性。在描述阶段，首先将检测到的特征的局部区域基于规范化的尺度和旋转划分为 4×4 个不重叠的网格，然后在每个单元格中进行包含 8 个箱的梯度方向直方图，并将其嵌入到 128 维的浮点向量中作为 SIFT 描述符。

另一个代表性的描述符是 SURF（Bay 等人 2006），它可以通过使用 Haar 小波响应来近似梯度计算来加速 SIFT 运算；此外，还应用积分图像来避免 Haar 小波响应中的重复计算，从而实现比 SIFT 更高效的计算。基于这两种方法的其他改进主要关注于提高辨别性、效率、鲁棒性以及应对特定图像数据或任务。例如，CSIFT（Abdel-Hakim 和 Farag 2006）使用额外的颜色信息来增强辨别性，ASIFT（Morel 和 Yu 2009）模拟了通过变化两个相机轴方向参数获得的所有图像视图，以实现完全仿射不变性。Mikolajczyk 和 Schmid（2005）使用极坐标分割和梯度方向直方图统计。SIFT-rank（Toews 和 Wells 2009）已被提出，用于基于 SIFT 的不变特征对应的序数图像描述。一种基于 Weber 定律的方法（WLD）（Chen 等人 2009）已被研究，用于在特定位置编码差分激发和方向的直方图。

Arandjelovi ́c 和 Zisserman（2012）使用了平方根（Hellinger）核函数来替代标准的欧几里德距离测量，将原始的 SIFT 空间转化为 RootSIFT 空间，并在不增加处理或存储要求的情况下获得了更好的性能。Dong 和 Soatto（2015）通过对不同域大小中的梯度方向进行池化，并提出了 DSP-SIFT 描述符，修改了 SIFT。基于 SIFT 的宽基线立体图像的另一种高效的密集描述符，即 DAISY（Tola 等人 2010），使用对数极坐标网格布局和高斯池化策略来近似梯度方向的直方图。受到 DAISY 的启发，DARTs（Marimon 等人 2010）可以高效地计算尺度空间并重用它来进行描述符计算，从而实现高效。最近还提出了一些手工制作的浮点型描述符，并表现出良好的性能；例如，局部重力力量模式（Bhattacharjee 和 Roy 2019）受到普遍引力定律的启发，可以看作是力量大小和角度的组合。

3.2.2 基于局部二值模式统计的描述符¶

与类似 SIFT 的方法不同，过去几十年中提出了一些基于强度统计的方法，这些方法受到局部二值模式（LBP）（Ojala 等人 2002）的启发。LBP 具有有利于其在兴趣区域描述中使用的特性，例如光照变化的容忍性和计算的简单性。缺点是该运算符产生了一个相当长的直方图，并且在平坦的图像区域中不太稳健。中心对称 LBP（CS-LBP）（Heikkilä等人 2009）（使用 SVM 进行分类器训练）是 LBP 的修改版本，结合了 SIFT 和 LBP 的优点，以解决平坦区域问题。具体来说，CS-LBP 使用了类似 SIFT 的网格，并用 LBP 基于特征的梯度信息替换了梯度信息。为了解决噪声问题，中心对称局部三值模式（CS-LTP）（Gupta 等人 2010）建议在块中使用相对顺序的直方图和 LBP 代码的直方图，例如相对强度的直方图。这两种基于 CS 的方法设计得比以前考虑的描述符更耐高斯噪声。RLBP（Chen 等人 2013）通过改变编码位来提高 LBP 的稳健性；已经开发了 LBP 运算符的完整建模和相关的完整 LBP 方案（Guo 等人 2010）用于纹理分类。类似的 LBP-like 方法广泛用于纹理表示和人脸识别领域，并且可以在综述文献中找到更多详细信息（Huang 等人 2011）。

3.2.3 基于局部强度比较的描述符¶

另一种描述符形式是基于局部强度比较的描述符，也称为二进制描述符，其核心挑战是用于比较的选择规则。由于其有限的区分度，这些方法大多限于短基线匹配。Calonder 等人（2010）提出了 BRIEF 描述符，它由图像块中多个随机点对的强度二进制测试结果串联而成。Rublee 等人（2011）在其 ORB 算法中提出了旋转 BRIEF，将其与定向 FAST 角点相结合，并使用机器学习策略选择了强大的二进制测试，以减轻旋转和尺度变化的限制。Leutenegger 等人（2011）开发了 BRISK 方法，使用了一个半径逐渐增大的同心圆采样策略。受视网膜结构启发，Alahi 等人（2012）提出了 FREAK 描述符，通过比较视网膜采样模式上的图像强度来进行快速计算和低内存成本的匹配，同时保持对尺度、旋转和噪声的鲁棒性。手工制作的二进制描述符和经典的机器学习技术也得到了广泛研究，这些将在基于学习的子节中介绍。

3.2.4 基于局部强度顺序统计的描述符¶

到目前为止，已经开发了许多方法，使用像素值的顺序而不是原始强度，实现了更有前景的性能（Tang 等人 2009；Toews 和 Wells 2009）。通过强度顺序的池化对旋转和单调强度变化不敏感，还将序数信息编码到描述符中；强度顺序池化方案可以使描述符在不估计参考方向的情况下具有旋转不变性，而对大多数现有方法而言，参考方向估计是主要的错误来源。为了解决这个问题，Tang 等人提出了序数空间强度分布（Tang 等人 2009）方法，该方法使用序数和空间强度直方图来归一化捕获的纹理信息和结构信息；该方法对任何单调递增的亮度变化都是不变的。

Fan 等人（2011）根据多个支持区域中的梯度和强度顺序对局部特征进行了池化，并提出了基于多支持区域顺序梯度直方图和多支持区域旋转和强度单调不变描述符方法。类似的策略在 LIOP（Wang 等人 2011，2015）中使用，以编码每个像素的局部顺序信息。在该工作中，使用整体序数信息将局部块划分为子区域，这些子区域用于累积 LIOP。LIOP 进一步改进为 OIOP/MIOP（Wang 等人 2015），可以编码用于噪声和畸变稳健性的整体序数信息。他们还提出了一种基于学习的量化方法来提高其区分度。

3.3 基于学习的特征描述符¶

手工制作的描述符，如上述所述，需要专业知识来设计，可能会忽略数据中隐藏的有用模式。这种要求促使对学习型描述符进行研究，由于其数据驱动的属性和有望的性能，近年来学习型描述符已经变得非常流行。接下来，我们将讨论在深度学习时代之前引入的一组经典学习型描述符。

3.3.1 经典学习型描述符¶

学习型描述符可以追溯到 PCASIFT（Ke 等人 2004），其中使用主成分分析（PCA）来通过减少由局部图像梯度组成的向量的维度，形成一个强大且紧凑的描述符。Cai 等人（2010）研究了使用线性判别投影来减少局部描述符的维度并提高可区分性的方法。Brown 等人（2010）引入了一个学习框架，其中使用 Powell 最小化和线性判别分析（LDA）技术来找到最优参数，用于构建描述符的一组构建块。Simonyan 等人（2014）提出了一种新颖的公式，将描述符学习中的空间池化和降维表示为基于 Brown 等人（2010）的工作的凸优化问题。同时，Trzcinski 等人（2012，2014）将增强技巧应用于从多个基于梯度的弱学习器学习增强的复杂非线性局部视觉特征表示。

除了上述的浮点型描述符，由于其低存储需求和高匹配速度等有益特性，二进制描述符在经典描述符学习中也备受关注。获取二进制描述符的一种自然方法是从提供的浮点型描述符中学习。这个任务通常通过哈希方法来实现，因此建议在新的空间中学习高维数据的紧凑表示时应保持它们的相似性。局部敏感哈希（LSH）（Gionis 等人 1999）可以说是一种常见的无监督哈希方法。该方法通过随机投影生成嵌入，并已用于许多大规模搜索任务。LSH 的一些变种包括核化 LSH（Kulis 和 Grauman 2009）、光谱哈希（Weiss 等人 2009）、语义哈希（Salakhutdinov 和 Hinton 2009）和基于 p 稳定分布的 LSH（Datar 等人 2004）。这些变种通常是无监督的。

监督哈希方法也已广泛研究，其中出现了不同的机器学习策略来学习针对特定任务定制的特征空间。在这种情况下，已经出现大量方法（Kulis 和 Darrell 2009；Wang 等人 2010；Strecha 等人 2012；Liu 等人 2012a；Norouzi 和 Blei 2011；Gong 等人 2013；Shakhnarovich 2005），其中图像匹配被认为是一个重要的实验验证任务。例如，Strecha 等人（2012）使用 LDA 技术来辅助哈希。Liu 等人（2012a）和 Wang 等人（2010）提出了半监督序贯学习算法，以找到具有区分性投影的方法。最小损失哈希（Norouzi 和 Blei 2011）基于具有潜在变量的结构 SVMs，提出了一种学习二进制哈希函数的新公式。Gong 等人（2012）提出了搜索零中心数据旋转以最小化将描述符映射到零中心二进制超立方体顶点的量化误差。

Trzcinski 和 Lepetit（2012）和 Trzcinski et al. (2017) 以直接从图像块中学习表示的简单方法开发了二进制描述符。在 Trzcinski 和 Lepetit（2012）中，他们提出了通过使用少量简单滤波器的线性组合来将图像块投影到判别子空间，然后阈值化其坐标以创建紧凑的二进制描述符。描述符的成功（例如 SIFT）在图像匹配期间表明，非线性滤波器（例如梯度响应）比线性滤波器更适合。Trzcinski 等人（2017）提出了一种学习具有与 AdaBoost 强分类器相同形式的哈希函数的方法，即每个描述符位的非线性弱学习器的线性组合的符号。这项工作比 Trzcinski 和 Lepetit（2012）更通用和强大，后者基于简单的阈值线性投影。Trzcinski 等人（2017）提出了生成独立适应于每个块的二进制描述符的方法。通过描述符的类间和类内在线优化来实现这个目标。

3.3.2 基于深度学习的描述符¶

使用深度技术的描述符通常被制定为一个监督学习问题。其目标是学习一种表示，使两个匹配的特征在测量空间中尽可能接近，而误匹配的特征在该空间中远离（Schonberger 等人 2017）。描述符学习通常通过在检测到的关键点周围裁剪的局部块上进行，因此也被称为块匹配。一般来说，现有方法包括两种形式，即度量学习（Weinberger 和 Saul 2009；Zagoruyko 和 Komodakis 2015；Han 等人 2015；Kedem 等人 2012；Wang 等人 2017；Weinberger 和 Saul 2009）和描述符学习（Simo-Serra 等人 2015；Balntas 等人 2016a，2017；Zhang 等人 2017c；Mishchuk 等人 2017；Wei 等人 2018；Heetal.2018；Tian 等人 2019；Luo 等人 2019），根据深度学习描述符的输出而言。这两种形式通常是联合训练的。具体来说，度量学习方法通常学习一个用于相似度测量的判别度量，其输入是原始块或生成的描述符。相比之下，描述符学习倾向于从原始图像或块生成描述符表示。这个过程需要一个测量方法，比如 L2 距离或经过训练的度量网络，用于相似性评估。与单一度量学习相比，使用 CNN 生成描述向量更加灵活，并且当有大量候选块可用于对应搜索时，可以避免重复计算，从而节省时间。由于其在信息提取和表征方面的强大能力，深度学习技术在特征描述方面取得了令人满意的性能。

使用深度学习技术的描述符可以被视为基于经典学习的描述符的扩展（Schonberger 等人 2017）。例如，Chopra 等人（2005）的 Siamese 结构以及常用的损失函数，如铰链损失、Siamese 损失、三元组损失、排名损失和对比损失，已被借鉴并修改为最近的深度方法。具体来说，Zagoruyko 和 Komodakis（2015）提出了他们的 DeepCompare，并演示了如何使用通用块相似性函数直接从原始图像像素中学习。在这种情况下，各种 Siamese 类型的 CNN 模型被应用于编码相似性函数。然后，这些模型被训练用于识别正样本和负样本图像块对。尝试的不同网络结构包括共享或不共享权重的 Siamese 和中心-周围形式。Han 等人（2015）提出了 MatchNet，用于同时学习描述符和度量。这样的技术通过级联类似 Siamese 的描述网络和完全卷积决策网络来实现。任务被转化为一个交叉熵损失下的分类问题。DeepDesc（Simo-Serra 等人 2015）使用 CNN 来学习具有 L2 距离测量的判别图像块表示。特别是，它通过最小化成对铰链损失来训练具有正样本和负样本块对的 Siamese 网络，提出的硬负采样策略减轻了正负样本不平衡问题。Wang 等人（2014）提出了一种新颖的深度排名模型，用于学习细粒度图像相似性。该模型采用了基于三元组的铰链损失和排名函数来刻画细粒度图像相似性关系。多尺度神经网络架构用于捕捉全局视觉属性和图像语义。

Kumar 等人（2016）首次使用全局损失来扩大正负样本块对之间的距离间隔。它通过三元组和 Siamese 网络的组合训练，其中包括三元组和全局损失。TFeat（Balntas 等人 2016b）建议利用三元组训练样本来进行基于 CNN 的图像块描述和匹配。它是通过浅卷积网络和快速硬负采样策略实现的。在 L2Net（Tian 等人 2017）中，Tian 等人应用了渐进采样策略来优化欧几里得空间中的相对距离损失函数。这项工作考虑了中间特征图和描述符的紧凑性以获得更好的性能。HardNet（Mishchuk 等人 2017）通过使用简单的铰链三元组损失和“最难在批次内”的挖掘比 L2Net 获得更好的改进。PN-Net（Balntas 等人 2016a）同时使用了在距离度量学习和在线增强领域引入的思想，通过同时使用正和负约束进行训练。所提出的 SoftPN 损失函数比铰链损失或 SoftMax 比率（Wang 等人 2014；Zagoruyko 和 Komodakis2015）具有更快的收敛速度和更低的误差。Zhang 等人（2017c）使用了全局正交正则化和三元组损失来训练他们的网络，以鼓励描述符足够“分散”。这是为了充分利用描述符空间。

基于平均精度关注的描述符学习（He 等人 2018）引入了一个通用的学习排名公式。该方法被定义为一种约束，其中真实匹配应排在所有虚假路径匹配之上，并且基于二进制和实值本地特征描述符进行优化。BinGAN（Zieba 等人 2018）提出了一种生成对抗网络（Goodfellow 等人 2014）的正则化方法，用于学习图像块的具有辨别性但紧凑的二进制表示。与之比较，Erin Liong 等人（2015）、Lin 等人（2016a）和 Duan 等人（2017）提出了关于二进制描述符学习的其他方法。除了损失函数、网络结构、正则化和硬负采样之外，Wei 等人（2018）通过使用核化子空间池化来学习具有区分性的深度描述符。Tian 等人（2019）在 SOSNet 中使用了二阶相似性。在 ContextDesc 中，一种更近期的方法，Luo 等人（2019）将局部块相似性约束与兴趣点的空间几何约束相结合，从而大大提高了匹配性能。

正如在基于 CNN 的检测器中提到的，越来越多的端到端学习方法将特征描述与检测器一起集成到完整的匹配流程中。这些方法类似于上述专门为描述而设计的方法。主要区别可能在于训练方式和整个网络结构的设计。核心挑战是使整个过程可微分并可训练。例如，LIFT（Yi 等人 2016）试图通过端到端 CNN 网络同时实现关键点检测、方向估计和特征描述。

SuperPoint（DeTone 等人 2018）提出了一种用于训练多视图几何问题的兴趣点检测器和描述符的自监督框架。完全卷积模型在全尺寸图像上运行，并共同计算像素级兴趣点位置和相关描述符，这与基于路径的网络形成对比。LF-Net（Ono 等人 2018）设计了一个双分支设置，并通过迭代创建虚拟目标响应，允许无需手工制作的先验条件即可从头开始进行训练。这个技术实现了特征图生成、使用前 K 选择和 NMS 的尺度不变关键点检测、方向估计和描述符提取。在 LF-Net 中，目标函数包括图像级损失（满足图像对、深度图和本质矩阵之间的附加约束）、面片级损失（学习对匹配有利的关键点，涉及方向和尺度组件几何一致性）以及描述符学习的三元组损失。

接下来，RF-Net（Shen 等人，2019）创建了一个端到端可训练的匹配框架，它是从 LF-Net 结构修改而来的。首先，构建的感知特征图导致了有效的关键点检测。其次，通用的损失函数术语，即邻域掩码，有助于训练补丁选择，以增强描述符训练的稳定性。D2-Net（Dusmanu 等人，2019）使用单个 CNN 同时实现了密集特征描述符和特征检测器的双重作用。在 Bhowmik 等人（2020）的研究中，使用强化学习的原理来优化关键点选择和描述符匹配，以解决高级别视觉任务下的问题。此外，Li 等人（2020）引入了双分辨率对应网络，通过提取不同分辨率的特征图以粗到精的方式来获取像素级对应关系。

除了为相同目标或场景进行特征匹配外，还研究了从相似目标/场景捕获的图像进行语义匹配，使用 CNN 并取得了显著的提升。语义匹配问题可能对手工制作的方法构成挑战，因为需要理解语义相似性。为此，UCN（Choy 等人，2016）使用深度度量学习直接学习了一个保留几何或语义相似性的特征空间。这种方法的使用还有助于生成几何或语义对应任务的密集和准确的对应关系。具体来说，UCN 实现了一个完全卷积的架构，具有对快速训练和测试的对应性对比损失，并提出了一个用于本地补丁标准化的卷积空间变换器。NCN（Rocco 等人，2018）开发了一种基于典型思想的可端到端训练的 CNN 架构，通过使用半本地约束来找到图像对之间可靠的稠密对应关系，这个框架通过分析全局几何模型的邻域共识模式来识别一对图像之间的空间一致性匹配集。该模型可以通过弱监督进行高效训练，无需任何点对应的手动注释。这种框架可以用于类别级和实例级匹配任务，而其他类似方法在 Han 等人（2017），Plötz 和 Roth（2018），Chen 等人（2018），Laskar 和 Kannala（2018），Kim 等人（2018, 2020），Ufer 和 Ommer（2017）和 Wang 等人（2018）的研究中也有提出。

3.4 三维特征描述符¶

目前已经有了大量关于三维特征描述符的研究。正如前面提到的，由于深度学习在许多不同领域的革命性成功，许多研究人员已经将注意力转向了深度学习范式。根据这一事实我们将现代描述符分为两组，即手工制作和基于学习的描述符。Guo 等人（2016）对传统的手工制作三维特征描述符进行了全面性能评估，而基于学习的方法则被忽略了。在接下来的部分中，我们将简要介绍最先进的手工制作描述符和基于学习的描述符。

3.4.1 手工制作三维描述符¶

Guo 等人（2016）将手工制作的描述符分为基于空间分布直方图和基于几何属性直方图的描述符，前者通过对支持区域中的点的空间分布进行编码的直方图来表示局部特征。通常，为每个关键点构建局部参考框架/轴。因此，将 3D 支持区域分成柱状图以形成直方图。每个柱的值是通过累积空间分布测量得出的。一些代表性的工作包括自旋图像（Johnson 和 Hebert 1999），三维形状上下文（Frome 等人 2004），独特形状上下文（Tombari 等人 2010a），旋转投影统计（Guo 等人 2013）和三自旋图像（Guo 等人 2015）。空间分布直方图描述符通过从支持区域中的几何属性（例如法线、曲率）的统计生成直方图来表示局部特征。这些直方图包括局部表面块（Chen 和 Bhanu 2007），THRIFT（Flint 等人 2007），点特征直方图（Rusu 等人 2008），快速点特征直方图（Rusu 等人 2009）和方向直方图签名（Tombari 等人 2010b）。除了几何属性和空间分布直方图描述符外，Zaharescu 等人（2009）引入了 MeshHoG 描述符，它类似于 SIFT（Lowe 2004），并使用梯度信息生成直方图。

光谱描述符，例如全局点签名（Rustamov 2007），HKS（Sun 等人 2009）和波核签名（WKS）（Aubry 等人 2011），在这个领域也占有重要地位。这些描述符是从与形状相关的 Laplace-Beltrami 算子的谱分解中获得的。全局点签名（Rustamov 2007）利用形状上的 Laplace-Beltrami 算子的特征值和特征函数来表示点的局部特征。HKS（Sun 等人 2009）和 WKS（Aubry 等人 2011）分别基于热扩散过程和形状上的量子力学粒子的时间演化。

3.4.2 基于学习的三维描述符¶

还有许多研究致力于使用不同的学习方案来泛化光谱描述符。Litman 和 Bronstein（2014）将光谱描述符泛化为一种通用家族，并提出了从示例中学习以获取特定任务的优化描述符的方法。这种学习方案类似于信号处理中 Wiener 滤波器的思想。Rodolà等人（2014）提出了一种学习方法，使波核描述符能够利用随机森林分类器从示例集中识别更广泛的变形类别。Windheuser 等人（2014）提出了一种度量学习方法，以改进光谱描述符的表示。现代深度学习技术也已成功应用。Masci 等人（2015）首次提出并介绍了将 CNN 范例泛化到非欧几何流形以进行形状对应的方法。随后，Boscaini 等人提出通过谱卷积网络（Boscaini 等人 2015）和各向异性 CNN（Boscaini 等人 2016）来学习描述符。Monti 等人（2017）提出了一个统一的框架，将 CNN 架构泛化到非欧几何领域（图和流形）。Xie 等人（2016）构建了一个深度度量网络，以形成用于形状表征的二进制光谱形状描述符。输入基于 Laplace-Beltrami 算子的特征值分解。

在空间域中，各种深度学习方法的差异通常在于所消耗数据的表示。Wei 等人（2016）在形状的深度图表示上训练了一个深度 CNN 以找到对应关系。Zeng 等人（2017）提出使用 3D 深度 CNN 来学习局部体积块描述符。该描述符消耗了局部区域的截断距离函数值的体素网格。Elbaz 等人（2017）提出了一个深度神经网络自编码器来解决三维匹配问题。作者使用了一个随机球面覆盖集算法来检测特征点，并将每个局部区域投影到深度图中，作为输入，用于生成描述符。Khoury 等人（2017）使用球面直方图参数化输入，以每个点为中心，并利用全连接的网络生成低维描述符。Georgakis 等人（2018）最近采用了一个处理深度图的 Siamese 架构网络。Zhou 等人（2018）提出了从多个视图的图像中学习三维关键点描述的方法。Wang 等人（2018b）将关键点的多尺度局部邻域参数化为常规的二维网格，作为三重架构 CNN 的输入。Deng 等人（2018）首次提出了一个基于 PointNet 的无序网络。这个网络可以消耗原始点云以充分利用三维匹配任务中的稀疏性。

3.5 总结¶

如前所述，图像块描述符的设计旨在实现检测到的特征点之间的准确和有效的对应关系建立。其目标是将原始图像信息转化为具有区分性和稳定性的表示，使两个匹配的特征尽可能接近，而误匹配的特征则相距甚远。为此，描述符应该易于计算，计算和存储要求低。这些描述符还应该在面对严重变形和成像条件时保持其区分性和不变性特征。在接下来的部分中，我们提供了对手工制作的描述符的全面分析，并介绍了学习方法如何部分应对这些挑战并实现有希望的性能的机制。

按照传统局部描述符的构建过程，第一步是提取低级信息，它可以简要分类为图像梯度和强度。具体来说，梯度信息可以被视为比原始强度更高阶的图像线索。通常需要池化策略以及直方图或统计方法来形成浮点描述符。因此，这种策略对几何变换更具不变性（也许是池化和统计策略使其更独立于像素位置和几何变化）。然而，它需要额外的计算来计算梯度和统计，以及浮点类型数据的距离度量。基于 LBP 的方法通常具有较高的区分能力和对光照变化和图像对比度的良好鲁棒性，因此经常用于纹理表示和人脸识别。

与基于梯度和/或统计的方法相比，基于图像强度的简单比较策略会牺牲很大的区分性和鲁棒性。经典的机器学习技术通常被设计用来识别实质性的有用位。这些类型的方法通常需要参考方向估计以实现旋转不变性，这似乎是大多数现有方法的主要错误源。然而，强度顺序的使用固有地对旋转和强度变化不变，而不需要任何几何估计。由于使用强度顺序和统计策略的结合，它可以实现可期的性能。

基于学习的方法很大程度上避免了手动经验和知识的先验要求。它们自动优化并获取最佳参数，并直接构建所需的描述符。传统的学习方法旨在使生成的描述符在效率、低存储和区分度方面更出色。然而，所使用的图像线索，如强度和梯度，仍然是低阶的，并且它们高度依赖于手工制作方法的框架。然而，当时出现的目标函数、训练技巧和数据集对于设计更好的基于学习的方法非常重要且有用。因此，深度学习的出现进一步推进了传统学习中的这个过程。

有几种技巧可以帮助提高深度描述符的区分能力和鲁棒性。一方面，中心周围和三元（甚至更多）结构可能提供大量的重要信息来学习。硬负样本挖掘策略会使结构集中在困难样本上（也可能导致过度拟合），因此可以实现更好的匹配性能。还应根据描述任务的基本和内在属性设计更可靠的损失函数。例如，最近设计的三元、排名、对比和全局损失优于早期的简单铰链和交叉熵损失。另一方面，也需要有效和全面的 ground truth 数据集，以获得更好的匹配性能和泛化能力。目前，将描述符与检测器一起训练，通过端到端方式构建成完整的匹配管道也引起了极大关注。这可以共同优化检测器和描述符，从而可以实现令人振奋的性能，并且其中的无监督训练可以在不需要任何标注的 ground truth 块数据的情况下进行。目前，使用深度技术，这些描述符可以在外观变化的图像对之间实现显著的匹配性能，例如光照和日夜。然而，这些描述符仍然受到严重几何变形的影响，例如大旋转或重叠较少的图像对。对于新类型数据的泛化能力较低也是另一个限制。

描述符的整体性能还取决于适当的检测器。不同的检测器和描述符的组合可能导致不同的匹配性能。因此，应根据特定任务和图像数据的类型选择描述符。使用深度学习的先进描述符已经显示出巨大的潜力。

4 匹配方法¶

匹配任务旨在在两幅图像之间建立正确的图像像素或点对应关系，无论是否使用特征检测和/或描述。这个任务在整个图像匹配流程中起着重要作用。针对特定应用和场景，引入了不同的匹配任务定义，可能展示出各自的优势。

4.1 匹配方法概述¶

在过去的几十年里，在图像匹配领域中，现有的方法大致可以分为两类，即基于区域和基于特征的方法（Zitova 和 Flusser 2003；Litjens 等人 2017）。基于区域的方法通常指的是密集匹配，也称为图像配准，通常不检测特征。在基于特征的方法中，当从图像对中提取特征点及其局部描述符时，图像匹配任务可以转化为以间接和直接的方式匹配它们，对应于使用和不使用局部图像描述符。

直接特征匹配旨在通过直接使用空间几何关系和优化方法从两组给定的特征集中建立对应关系，这可以粗略地分为图匹配和点集配准两类。相比之下，间接特征匹配方法通常将匹配任务分为两个阶段的问题。这种任务通常从通过测量空间的距离来评估描述符的相似性开始，建立初步对应关系。然后，通过使用额外的局部和/或全局几何约束将错误匹配从潜在匹配集中移除。从稀疏特征对应关系中进行的密集匹配通常需要进行变换模型估计的后处理，然后进行图像重采样和插值（变换）。

我们将基于学习的方法与基于区域和基于特征的方法分开，并在新一小节中介绍它们。从输入数据的角度来看，从图像和从点数据中学习是基于学习的匹配的两种主要形式。与传统方法相比，这些方法在某些情景下可以实现更好的性能。本节还简要介绍了三维情况下的匹配任务。

4.2 基于区域的匹配¶

基于区域的方法旨在进行图像配准，并通过直接使用整个图像的像素强度来建立密集像素对应关系。需要使用相似性度量标准以及优化方法来估计几何变换并通过最小化目标图像和变换后移动图像之间的总不相似度来进行公共区域对齐。因此，通常使用多种手动相似性度量标准，包括类似于相关性的方法、域变换和互信息（MI）方法。还需要优化方法和变换模型来执行最终的配准任务（Zitova 和 Flusser 2003）。

在图像配准领域中，类似于相关性的方法被视为基于区域的方法中的经典代表，它通过最大化两个滑动窗口的相似性来对应两幅图像（Zitova 和 Flusser 2003；Lietal.2015）。例如，已开发了基于小波特征的最大相关性用于自动注册（Le Moigne 等人 2002）。然而，这种方法可能会在严重的图像变形情况下遇到困难（只有在存在轻微旋转和缩放时才能成功应用），包含平滑区域而没有明显细节的窗口以及巨大的计算负担。

域变换方法倾向于在将原始图像转换为另一个域（例如，基于 Fourier 移位定理的相位相关）的基础上对齐两幅图像（Reddy 和 Chatterji 1996；Liu 等人 2005；Chen 等人 1994；Takita 等人 2003；Foroosh 等人 2002）以及基于 Walsh 变换的方法（Lazaridis 和 Petrou 2006；Pan 等人 2008）。这些方法对相关和频率相关的噪声以及非均匀的、时间变化的照明干扰具有鲁棒性。然而，在图像对具有明显不同的光谱内容和小重叠区域的情况下，这些方法存在一些限制。

基于信息理论，如使用 MI 进行非刚性图像配准，结合 B 样条（Klein 等人 2007）和条件 MI（Loeckx 等人 2009），是两幅图像之间的统计依赖性的测量，并应用于整个图像（Maes 等人 1997）。因此，MI 特别适用于多模态（Chen 等人 2003a、b；Johnson 等人 2001）的注册。最近，Cao 等人（2020）提出了一种结构一致性增强变换，用于增强多光谱和多模态图像配准问题中的结构相似性，从而避免了光谱信息失真。然而，MI 在确定整个搜索空间的全局最大值方面存在困难，这不可避免地降低了其鲁棒性。此外，优化方法（例如，连续优化、离散优化以及它们的混合形式）和变换模型（例如，刚性、仿射、薄板样条（TPS）、弹性体和扩散模型）被认为已经足够成熟。请参阅 Zitova 和 Flusser（2003）、Dawn 等人（2010）、Sotiras 等人（2013）和 Ferrante 和 Paragios（2017）以获取代表性文献和更多细节。

基于区域的方法对于医学或遥感图像注册是可以接受的，因为许多基于特征的方法不再可行，因为这些图像通常包含较少的纹理细节和由于不同的成像传感器而导致的图像外观的大方差。然而，基于区域的方法可能会在严重的几何变换和局部变形情况下遇到困难。深度学习已经证明了其有效性，其中早期的方法通常被用作经典注册框架的直接扩展，而后期方法使用强化学习范式来迭代地估计变换，甚至以端到端的方式直接估计变形场。带有学习策略的基于区域的匹配将在学习匹配的部分中进行审查。

4.3 图匹配方法¶

给定从图像提取的特征点，我们可以通过将每个特征点与节点关联并指定边来构建一个图。这个过程自然地为研究图像数据的内在结构提供了方便，特别是对于匹配问题。根据这一定义，图匹配（GM）是指在两个或多个图之间建立节点到节点的对应关系。由于其重要性和基本挑战，GM 已经是一个长期存在的研究领域，研究人员仍然对其有极大的兴趣。从问题设置的角度来看，GM 可以分为两类，即精确匹配和不精确匹配。精确匹配方法将 GM 视为图或子图同构问题的一种特殊情况。它旨在找到两个二进制（子）图的双射；因此，所有边都是严格保留的（babai2018groups,cook2006mining,levi1973note）。实际上，这个要求对于计算机视觉等现实任务来说过于严格。因此，研究人员通常转向具有节点和边权重属性的不精确匹配。这种方法在实践中具有很好的灵活性和实用性。因此，我们主要集中在对不精确匹配方法的回顾中。

在某种程度上，GM 具有特征匹配问题的简单而通用的表述，它将几何线索编码为节点亲和力（一阶关系）和边亲和力（二阶关系），以推导出两个图之间的真实对应关系。除了几何线索外，特征点的高级信息也可以并入 GM 中（例如，将描述符相似性作为节点亲和力）。这些信息只作为补充信息，不是必需的。在一般和最近的形式中，GM 可以被公式化为二次分配问题（QAP）（Loiola 等人 2007）。尽管文献中存在不同的形式，但研究的主体集中在 Lawler 的 QAP（Lawler 1963）上。给定两个图 \(G_1 =(V_1,E_1)\) 和 \(G_2 =(V_2,E_2)\)，其中 \(|V_1|=n_1\)，\(|V_2|=n_2\)，每个节点 \(v_i \in V_1\) 或 \(v_j \in V_2\) 表示一个特征点，每个边 \(e_i \in E_1\) 或 \(e_j \in E_2\) 定义在一对节点上。在不失一般性的情况下，我们假设 \(n_1 \ge n_2\)，Lawler 的 QAP 形式的 GM 可以写为：

其中 \(\mathbf{X}\) 表示排列矩阵，即 \(\mathbf{X}_{ij} = 1\) 表示节点 \(v_i \in V_1\) 对应于节点 \(v_j \in V_2\)，否则 \(\mathbf{X}_{ij} = 0\) ，\(\mathrm{vec}(\mathbf{X})\) 表示 \(\mathbf{X}\) 的列向量化，\(\mathbf{1}_{n_1}\) 和 \(\mathbf{1}_{n_2}\) 分别表示所有 1 的列向量，\(\mathbf{K}\) 表示亲和力矩阵，其对角线和非对角线条目编码两个图之间的一阶和二阶边亲和力。没有通用的方法可以用来构建亲和力矩阵；然而，一个简单的策略是使用特征描述符的相似性，【例如 Shape Context（Belongie 等人 2001）】和边长的差异来确定节点和边的亲和力。

Koopmans-Beckmann 的 QAP 是另一种流行的形式。这个形式与 Lawler 的 QAP 不同，如下所示：

其中 \(\mathbf{A}_1\) 和 \(\mathbf{A}_2\) 分别是两个图的加权邻接矩阵，\(\mathbf{K}_p\) 是节点亲和力矩阵。在 Zhou 和 De la Torre（2015）中，研究了 Koopmans-Beckmann 的 QAP 与 Lawler 的 QAP 之间的关系，揭示了 Koopmans-Beckmann 的 QAP 可以被视为 Lawler 的 QAP 的特殊情况。 GM 问题被转化为寻找最优的一对一对应关系 \(\mathbf{X}\) ，以最大化整体亲和度得分 \(J(\mathbf{X})\) 。作为一般的组合 QAP 问题，GM 已知是 NP 困难问题。大多数方法放宽了严格的约束并以可接受的代价提供了近似解决方案。在这方面，文献中引入了许多放宽策略，因此产生了各种各样的 GM 求解器。接下来，我们通过 GM 的发展过程简要回顾了一些有影响力的方法。

4.3.1 光谱松弛方法¶

第一组方法采用光谱松弛策略。Leordeanu 和 Hebert（2005）提出用约束 \(\|\mathrm{vec(X)}\|^2_2 = 1\) 来代替一对一映射约束和二进制约束。在这种情况下，可以通过解特征向量问题来获得解 \(\mathbf{X}\)。\(\mathbf{X}\) 中的每个元素都被解释为一对应关系与最佳聚类（真实对应关系）的关联。采用离散化策略来强制执行映射约束。这个想法后来被 Cour 等人（2007）改进，他们明确考虑了强制执行一对一映射约束以实现更紧密的松弛。这种方法也可以作为特征向量问题的封闭形式来解决。Liu 和 Yan（2010）提出了一种基于 \(l_1\) 范数的光谱松弛技术，即约束 \(\|\mathrm{vec(X)}‖_1 = 1\) 来检测多个视觉模式。解决方案可以通过进化博弈理论中的复制器方程有效地获得。Jiang 等人（2014）提出了一种非负矩阵分解技术，将约束扩展为 \(\|\mathrm{vec(X)}\|_p = 1\)，其中 \(p \in [1, 2]\)。与此同时，Egozi 等人（2012）提出了一种截然不同的方法。在他们的工作中，他们提供了光谱匹配方案的概率解释，并推导出一种新的概率匹配方案，其中亲和力矩阵也在迭代过程中更新。使用 Koopmans-Beckmann 的 QAP 公式，光谱方法（Umeyama 1988; Scott 和 Longuet-Higgins 1991; Shapiro 和 Brady 1992; Caelli 和 Kosinov 2004）将 \(\mathbf{X}\) 松弛为正交，即 \(\mathbf{X}^\mathrm{T} \mathbf{X} = \mathbf{I}\)。这个表达式可以作为特征值问题封闭形式解决。这些方法由于松弛程度较大而具有效率的优点。然而，一般情况下精度不足。

4.3.2 凸松弛方法¶

许多研究已经转向研究原始问题的凸松弛方法，以获得解决非凸 QAP 问题的理论优势。通过添加表示原始变量中二次单项式的辅助变量的升级方法可以获得强凸松弛。这允许在升级变量上添加附加的凸约束。半定规划（SDP）是解决组合问题的通用工具，已应用于解决 GM（Schellewald 和 Schnörr 2005; Torr 2003; Zhao 等 1998; Kezurer 等 2015）。SDP 松弛非常紧密，允许在多项式时间内找到强近似解。然而，高计算成本限制了其可扩展性。还有一些具有线性规划松弛的其他升级方法（Almohamad 和 Duffuaa 1993; Adams 和 Johnson 1994）。最近广泛考虑了 LP 松弛的对偶问题来解决 GM（Swoboda 等人 2017; Chen 和 Koltun 2015; Swoboda 等人 2017; Torresani 等人 2012; Zhang 等人 2016），这与 MAP 推断算法有很强的联系。

4.3.3 凸到凹松弛¶

一个有用的策略是利用路径跟随技术。这种方法逐渐实现了原始问题的凸到凹过程，最终找到一个满足约束的良好解决方案。与升级方法相比，计算复杂度也低得多。Zaslavskiy 等人（2009）采用了这种策略来解决 Koopmans-Beckmann 的 QAP 公式的 GM 问题，该公式被扩展到有向图（Liu 等人 2012b）和部分匹配（Liu 和 Qiao2014）。Zhou 和 De la Torre（2015）提出了一个基于 Lawler 的 QAP 的亲和矩阵因子分解技术的统一框架。这样的框架有效地降低了计算复杂度，并揭示了 Koopmans-Beckmann 和 Lawler 的 QAP 之间的关系。 （高级）双随机（DS）松弛方法通过识别更紧密的公式（Fogel 等人 2013; Dym 等人 2017; Bernard 等人 2018）改进了这些方法，其中谈到了光谱、SDP 和 DS 松弛的紧密度，并在理论上得到了验证。

4.3.4 连续松弛¶

大量的 GM 方法侧重于设计用于近似解决 QAP 的准确或高效算法，尽管没有全局最优性保证。在大多数情况下，\(\mathbf{X}\) 被简单地松弛为连续的 DS 矩阵。Gold 和 Rangarajan（1996）提出了一种渐进分配算法，它在退火进程下对松弛问题进行梯度上升。这种方法的收敛性已经被 Tian 等人（2012）重新审视并改进，采用了软约束机制。van Wyk 和 van Wyk（2004）提出了通过逐渐投影到所需整数约束的凸集来强制执行一对一映射约束的方法。Leordeanu 等人（2009）提出了一种有效的算法，通过解一系列线性分配问题来在（准）离散域中进行优化。还测试了许多著名的优化技术，如 ADMM（Lê-Huu 和 Paragios 2017）、禁忌搜索（Adamczewski 等人 2015）和乘法更新算法（Jiang 等人 2017a）。最近的研究还包括 Jiang 等人（2017b）和 Yu 等人（2018），它们引入了新的方案来渐近地近似原始的 QAP，以及 Maron 和 Lipman（2018），它提出了一种新的（可能是）凹松弛技术。Yu 等人（2020b）引入了一种行列式正则化技术，结合了基于梯度的优化，将这个问题松弛到连续域中。

4.3.5 多图匹配¶

与经典的两图匹配设置不同，联合匹配一批具有一致对应关系的图，即多图匹配，近年来引起了越来越多的关注，因为它在方法论上具有优势，可以融合跨图信息。多图匹配的一个核心问题是为可行解决方案强制执行循环一致性。一般来说，这个概念是指两个图之间的双射对应关系应该与通过中间图导出的双射对应关系一致。更具体地说，对于任何一对图 \(G_a\) 和 \(G_b\)，其节点对应矩阵 \(\mathbf{X}^{ab}\)，令 \(G_c\) 为中间图，循环一致性约束被强制执行： \(\mathbf{X}^{ac}\mathbf{X}^{cb} = \mathbf{X}^{ab}\)，其中 \(\mathbf{X}^{ac}\) 和 \(\mathbf{X}^{cb}\) 分别是 \(G_a\) 和 \(G_c\) 以及 \(G_c\) 和 \(G_b\) 的匹配解决方案。

现有的多图匹配方法可以大致分为三类。对于属于第一组的方法，多图匹配问题通过计算一系列二图匹配任务的迭代过程来解决（Yan 等人 2013、2014、2015a，b; Jiang 等人 2020b）。在每次迭代中，计算二图匹配解决方案，以局部最大化亲和分数，这可以利用现成的二元匹配求解器，比如 Jiang 等人（2020b）中，同时考虑离线批处理模式和在线设置，以探索通过二元匹配实现循环一致性的概念。另一组工作以初始（带噪声的）二图匹配结果作为输入，并旨在恢复全局一致的二图匹配集（Kim 等人 2012; Pachauri 等人 2013; Huang 和 Guibas2013; Chen 等人 2014; Zhou 等人 2015; Wang 等人 2018; Hu 等人 2018）。在这些方法中，同时考虑了所有图的匹配，以形成包含所有二图匹配的大矩阵。由匹配问题引发的这个矩阵的固有结构，如循环一致性等，得到了研究。最后一组利用聚类或低秩恢复技术来解决多图匹配问题，为问题提供了特征空间的新视角（Zeng 等人 2012; Yan 等人 2015c, 2016a; Tron 等人 2017）。最近，多图匹配问题已被考虑为一个在理论上有坚实基础的凸松弛（Swoboda 等人 2019），或使用投影功率迭代搜索可行解决方案的优化框架（Bernard 等人 2019）。

4.3.6 其他范式¶

尽管 QAP 公式在 GM 中很常见，但制定方式并不唯一。许多方法从不同的角度或范式处理 GM，并在这个领域中形成了重要的类别。Cho 等人（2010）提出了 GM 的随机漫步观点，并设计了一种通过模拟关联图上的随机漫步来获得解决方案的技术。Lee 等人（2010）和 Suh 等人（2012）引入了蒙特卡罗方法来提高匹配的稳健性。Cho 和 Lee（2012）进一步设计了一种渐进的 GM 方法，它将图的进展与图的匹配相结合，以降低计算复杂性。Wang 等人（2018a）提出了使用图的功能表示，并通过最小化原始图和变换后的图之间的差异来进行匹配的方法。随后，为了抑制异常值的匹配，Wang 等人（2020）将潜在的异常值分配为获得的最优对应关系矩阵中的零向量。亲和矩阵在 GM 问题中起着关键作用。然而，手工制作的 \(\mathbf{K}\) 容易受到尺度和旋转差异的影响。为此，设计了无监督方法（Leordeanu 等人 2012）和有监督方法（Caetano 等人 2009）来学习 \(\mathbf{K}\) 。Zanfir 和 Sminchisescu（2018）最近通过端到端的深度学习方案解决了这个问题。Wang 等人（2020）引入了一个完全可训练的图匹配框架。在这个框架中，他们利用了图网络块模块，并同时考虑了节点/边亲和力的学习和组合优化的求解。

将 GM 扩展到高阶公式是通过主要探索几何线索来提高鲁棒性的自然方式。这导致了一种基于张量的目标（Lee 等人 2011），也称为超图匹配

其中 \(m\) 是亲和度的阶数，\(\mathbf{H}\) 表示编码图中超边之间亲和度的 \(m\) 阶张量， \(\otimes_k\) 是张量乘积，\(\mathbf{x} = \mathrm{vec(X)}\) 。超图匹配的代表性研究包括 Zass 和 Shashua（2008），Chertok 和 Keller（2010），Lee 等人（2011），Chang 和 Kimia（2011），Duchenne 等人（2011）和 Yan 等人（2015d）。

4.4 点集配准方法¶

点集配准（PSR）旨在估计最佳对齐两个点集的空间变换。在特征匹配中，PSR 和 GM 采用不同的公式。对于两个点集，GM 方法通过最大化一元对应和成对对应的整体亲和度分数来确定对齐。相比之下，PSR 方法确定了底层的全局变换。给定两个点集 \(\{\mathrm{x_i}\}^{n_1}_{ i=1}\) 和 \(\{\mathrm{y_i}\}^{n_2}_{ i=1}\) ，通常的目标可以表示为：

其中θ表示预定义变换的参数。正则化项 g（P）避免了平凡解，比如 P = 0。与 GM 相比，这个模型只表示一般原则，但不一定涵盖所有的 PSR 算法。例如，可以使用概率解释或基于密度的目标，并且在优化过程中可能只部分强加 P 的约束，这与上述公式不同。

PSR 对数据提出了更强的假设，即点集之间存在全局变换，这是将其与 GM 区分开的关键特征。尽管通用性受到限制，但这一假设导致了低计算复杂性，因为全局变换模型需要较少的参数。从刚性到非刚性的复杂变换模型被开发出来，以增强泛化能力。还提出了各种方案来提高对降解的鲁棒性，如噪声、异常值和丢失点。

4.4.1 ICP 及其变种¶

PSR 已经成为计算机视觉领域的一个重要研究课题，迭代最近点（ICP）算法是一种流行的方法（Besl 和 McKay 1992）。ICP 交替进行两个点集中最接近点的硬分配和封闭形式刚性变换估计，直到收敛。由于其简单性和低计算复杂性，ICP 算法被广泛用作基线算法。然而，ICP 需要良好的初始化，因为它容易陷入局部最优解。在 PSR 领域，已经提出了许多研究，如 EM-ICP（Granger 和 Pennec 2002），LM-ICP（Fitzgibbon 2003）和 TriICP（Chetverikov 等人 2005），以改进 ICP。可以参考最近的一项调查（Pomerleau 等人 2013）来详细讨论 ICP 的变种。鲁棒点匹配（RPM）算法（Gold 等人 1998）被提出来克服 ICP 的限制；采用了软分配和确定性退火策略，而刚性变换模型则通过使用薄板样条【TPS-RPM（Chui 和 Rangarajan 2003）】来进行非刚性化。

4.4.2 基于 EM 的方法¶

RPM 也是 EM 类 PSR 方法的代表之一，它们在该领域占据重要地位。这些 EM 类方法将 PSR 问题建模为加权平方损失函数或高斯混合模型（GMMs）的对数似然最大化的优化问题，然后通过 EM 或 EM 类算法来搜索局部最优解。在 E 步骤中计算每个对应关系的后验概率，然后在 M 步骤中对变换进行细化。Sofka 等人（2007）研究了在配准过程中建模不确定性，并提出了一个在 EM 类框架下的协方差驱动的对应方法。Myronenko 和 Song（2010）提出了著名的一致性点漂移（CPD）方法，该方法建立在 GMM 基础上的概率框架中；在这里，EM 算法用于参数的最大似然估计。Horaud 等人（2011）开发了一种基于期望条件极大化的概率方法，允许在混合模型成分中使用各向异性协方差，并改善了各向同性协方差情况下的性能。Ma 等人（2016b）和 Zhang 等人（2017a）在 GMM-based 概率框架中利用了局部特征和全局特征的统一性。Lawin 等人（2018）通过潜在的场景结构的概率分布来提出了一种密度自适应的 PSR 方法。

4.4.3 基于密度的方法¶

基于密度的方法引入了生成模型到 PSR 问题中，其中不建立明确的点对应关系。每个点集通过密度函数（如 GMM）来表示，配准通过最小化两个密度函数之间的统计差异度量来实现。Tsin 和 Kanade（2004）首次提出了这种方法，并使用核密度函数来建模点集，差异度量定义为核相关性。与此同时，Glaunes 等人（2004）使用了弛豫的 Dirac delta 函数来表示点集。然后，他们确定了最优的微分同胚变换，以最小化两个分布的距离。Jian 和 Vemuri（2011）扩展了这一方法，采用了基于 GMM 的表示，并最小化了密度之间的 L2 误差。作者还提供了基于密度的 PSR 的统一框架。许多流行的方法，包括 Myronenko 和 Song（2010）和 Tsin 和 Kanade（2004），从理论上来说可以被视为特殊情况。Campbell 和 Petersson（2015）提出了使用支持向量参数化的 GMM 进行自适应数据表示。这种方法可以提高基于密度的方法对噪声、异常值和遮挡的鲁棒性。最近，Liao 等人（2020）利用模糊聚类来表示扫描点集，然后通过最小化两个模糊聚类中心之间的模糊加权距离和来对两个点集进行配准。

4.4.4 基于优化的方法¶

一组基于优化的方法已被提出作为全局最优解，以缓解局部最优问题。这些方法通常在有限的变换空间中进行搜索，以节省时间，例如旋转、平移和缩放。广泛使用随机优化技术，包括遗传算法（Silva 等人 2005；Robertson 和 Fisher 2002）、粒子群优化（Li 等人 2009）、粒子滤波（Sandhu 等人 2010）和模拟退火方案（Papazov 和 Burschka 2011；Blais 和 Levine 1995），但不能保证收敛。与此同时，分支界限（BnB）是一种良好建立的优化技术，可以在变换空间中高效地搜索全局最优解，并构成许多基于优化的方法的理论基础，包括 Li 和 Hartley（2007）、Parra Bustos 等人（2014）、Campbell 和 Petersson（2016）、Yang 等人（2016）和 Liu 等人（2018b）。除了这些方法之外，Maron 等人（2016）引入了一种基于半定规划（SDP）松弛的方法，该方法保证了等距形状匹配的全局解。Lian 等人（2017）通过消除刚性变换变量，将 PSR 公式化为凹形 QAP，并利用 BnB 来实现全局最优解。Yao 等人（2020）提出了一种鲁棒非刚性 PSR 的公式，基于全局平滑鲁棒数据拟合和正则化，通过 majorization-minimization 算法进行优化，以减少解决简单最小二乘问题的每次迭代。Iglesias 等人（2020）的另一种方法介绍了 PSR 的缺失数据的全局最优性条件。这种方法应用 Lagrange 对偶性生成原始问题的候选解，从而使其能够以闭合形式获得对应的对偶变量。

4.4.5 杂项方法¶

除了基于刚性模型或基于 TPS（Chui 和 Rangarajan 2003）或高斯径向基函数（Myronenko 和 Song 2010）的非刚性变换模型之外，文献中还考虑了其他复杂的变形模型。这些模型包括简单的关节扩展，如 Horaud 等人（2011）和 Gao 和 Tedrake（2019）。在非刚性 ICP（Amberg 等人 2007）中，引入了平滑的局部仿射模型作为变换模型，并在 ICP 框架下进行开发，这也被采用在 Li 等人（2008）的工作中。然而，这个模型应该与稀疏手动选择的特征对应关系一起使用，因为它允许多自由度。另一个不同的线性蒙皮模型，不需要用户参与配准过程，在另一项工作中提出并应用（Chang 和 Zwicker 2009）。PSR 方法的另一条线路将形状描述符引入到配准过程中。本地形状描述符，如自旋图像（Johnson 和 Hebert 1999）、形状上下文（Belongie 等人 2001）、积分体积（Gelfand 等人 2005）和点特征直方图（Rusu 等人 2009），被生成。通过描述符的相似性约束建立稀疏特征对应关系。随后，可以使用随机抽样一致性（RANSAC）（Fischler 和 Bolles 1981）或 BnB 搜索（Bazin 等人 2012）来估计基础刚性变换。Ma 等人（2013b）提出了一种基于非刚性情况下的 \(L_2E\) 估计器的鲁棒算法。

PSR 基于不同观察的一些新方案已经出现。Golyanik 等人（2016）将点集建模为受引力作用的粒子，通过求解牛顿力学的微分方程来实现配准。Ma 等人（2015a）和 Wang 等人（2016）提出了使用上下文感知高斯场来解决 PSR 问题。Vongkulbhisal 等人（2017，2018）提出了区分性优化方法。这种方法从训练数据中学习搜索方向，以指导优化，无需定义成本函数。Danelljan 等人（2016）和 Park 等人（2017）考虑了点集的颜色信息，而 Evangelidis 和 Horaud（2018）以及 Giraldo 等人（2017）解决了多个点集的联合配准问题。

4.5 消除误匹配的描述符匹配¶

描述符匹配后的误匹配消除，也称为间接图像匹配，将匹配任务分为两个阶段的问题。这种方法通常从通过测量空间的距离来计算局部图像描述符的相似性，建立初步对应关系开始。构建虚拟匹配集的常见策略包括固定阈值（FT）、最近邻（NN，也称为蛮力匹配）、互相最近邻（MNN）和最近邻距离比（NNDR）。然后，通过使用额外的局部和/或全局几何约束，从虚拟匹配集中移除错误匹配。我们将误匹配消除方法简要分为基于重新采样的方法、非参数模型方法和宽松方法。在接下来的章节中，我们将详细介绍这些方法并进行全面分析。

4.5.1 虚拟匹配集构建¶

假设我们已经从考虑的两幅图像 \(I_1\) 和 \(I_2\) 中检测和提取了 \(M\) 和 \(N\) 个要匹配的局部特征。描述符匹配阶段通过计算具有 \(M\times N\) 个条目的成对距离矩阵来运作，然后通过上述规则选择潜在的真实匹配项。FT 策略考虑了距离低于固定阈值的匹配项。然而，这种策略可能会对数据敏感，并可能导致与一对一对应性相反的众多一对多匹配。这种情况会导致特征匹配任务性能不佳。NN 策略可以有效处理数据敏感性问题并提高潜在真实匹配项的召回率。这种策略已经应用于各种描述符匹配方法中，但它无法避免一对多的情况。在互相最近邻描述符匹配中， \(I_1\) 中的每个特征寻找其在 \(I_2\) 中的最近邻（反之亦然），成为虚拟匹配集中的候选匹配项。这种策略可以获得高比例的正确匹配，但可能牺牲了许多其他真实对应关系。NNDR 考虑到了第一个和第二个最近邻之间的距离差异很大。因此，使用预定义的阈值的距离比会获得稳健且有前途的匹配性能，而不会牺牲许多真实匹配。然而，尽管 NNDR 方法在 SIFT 等描述符匹配中被广泛使用且表现良好，但它仍然依赖于这些描述符的稳定距离分布。实际上，NNDR 对于其他类型的描述符，如二进制或一些基于学习的描述符（Rublee 等人 2011；Ono 等人 2018），已不再适用。

选择这些描述符匹配方法的最佳方法应取决于描述符的属性和特定应用场景。例如，MNN 比其他方法更严格，具有更高的内点比率，但可能会牺牲许多其他潜在真实匹配。相比之下，NN 和 NNDR 在特征匹配任务中往往更通用，性能相对更好。Mikolajczyk 和 Schmid（2005）提出了有关这些候选匹配选择策略的简单测试。尽管可以用于构建虚拟特征对应关系的各种方法都可用，但仅使用本地外观信息和基于相似性的简单虚拟匹配选择策略，将不可避免地导致大量不正确的匹配，特别是当图像经历严重的非刚性变形、极端视角变化、低质量和/或重复内容时。因此，在第二阶段迫切需要一种强大、精确和高效的误匹配消除方法，以尽可能保留尽可能多的真实匹配，同时通过使用额外的几何约束来将误匹配降到最低。

4.5.2 基于重新采样的方法¶

重新采样技术是一种流行的范式，由经典的 RANSAC 算法（Fischler 和 Bolles 1981）代表。基本上，假设这两幅图像由某种参数化几何关系（如射影变换或极线几何）耦合在一起。然后，RANSAC 算法采用一种假设和验证策略：反复从数据中采样最小子集，例如射影变换的四个对应关系和基础的七个对应关系，作为假设估计模型，并通过一致内点数量验证质量。最终，与最优模型一致的对应关系被识别为内点。

已经提出了各种方法来提高 RANSAC 的性能。在 MLESAC（Torr 和 Zisserman 1998，2000）中，通过最大似然过程来验证模型质量，尽管在某些假设下，它可以改进结果并对预定义的阈值不太敏感。修改验证阶段的想法不仅仅是用于简单实现，而且在许多后续研究中进一步扩展。由于具有吸引人的效率提高结果，采样策略的修改也在很多研究中考虑。实际上，各种先验信息被纳入，以增加选择全内点样本子集的概率。具体来说，内点被假定在 NAPSAC（Nasuto 和 Craddock 2002）中在空间上是连贯的，或者在 GroupSAC（Ni 等人 2009）中存在某些分组。PROSAC（Chum 和 Matas 2005）利用了先验预测的内点概率，EVSAC（Fragoso 等人 2013）使用了与对应关系的极值理论的置信度估计。另一个具有里程碑意义的工作是局部优化的 RANSAC（LO-RANSAC）（Chum 等人 2003），其中关键观察是当到达迄今为止最佳模型时，采用最小子集可以放大底层噪声并产生与 ground truth 相去甚远的假设。在原始论文中，局部优化被实现为一个迭代的最小二乘拟合过程，其中内点外点阈值在内部 RANSAC 中缩小。这具有比最小采样大的成本，仅应用于当前模型的内点。LO-RANSAC 的计算成本问题在 Lebeda 等人（2012）中得到了解决，其中建议了几种实施改进。局部优化步骤在 Barath 和 Matas（2018）中采用了图割技术进行扩展。许多改进 RANSAC 的策略都集成在 USAC（Raguram 等人 2012）中。

最近，Barath 等人（2019b）在他们的 MAGSAC 中应用了 \(\sigma\)-一致性，通过在一系列噪声尺度上进行边际化来消除对用户定义阈值的需求。此后，Barath 等人（2019a）观察到附近的点更有可能来自相同的几何模型，通过从逐渐扩大的邻域中提取样本，他们提取了全局采样和参数模型估计的局部结构。基于上述两种方法，他们引入了 MAGSAC++（Barath 等人 2020）并引入了一个新的评分函数。这种方法避免了需要内点/外点决策，其中一种新颖的边际化过程被构建为 M-估计，通过迭代重新加权最小二乘过程来解决，Barath 等人（2019a）中的渐进增长采样策略也应用于类似 RANSAC 的鲁棒估计。

尽管重新采样方法在计算机视觉的广泛应用中非常有效，但它们存在一些基本缺陷。例如，理论上所需的运行时间随着异常值率的增加呈指数级增长。最小子集采样策略仅适用于参数模型，并不能处理经历复杂变换的图像对，例如非刚性变换。这种情况激发了研究人员开发脱离重新采样范式的新算法。

4.5.3 基于非参数模型的方法¶

已经提出了一组非参数模型方法。与简单的参数模型不同，非参数模型处理匹配中更一般的先验，例如运动连贯性，并且可以处理退化情况。这些方法通过不同的变形函数来建模变换，通过不同的方式处理严重异常值来进行区分。Pilet 等人（2008）提出使用三角形化的 2-D 网格来模拟变形，使用定制的鲁棒估计器来消除异常值的有害影响。鲁棒估计器的思想也在 Gay-Bellile 等人（2008）中利用 Huber 估计器和 Ma 等人（2015）中使用 L2 E 估计器中得到了应用，尽管它们对变形建模不同。在 Li 和 Hu（2010）中提出了一种完全不同的方法，其中采用支持向量回归技术来稳健地估计对应关系函数并拒绝误匹配项。

有创造力的矢量场一致性（VFC）（Ma 等人 2013a，2014）是非刚性匹配的一个新框架。变形函数限制在再生核希尔伯特空间中，与 Tikhonov 正则化一起用于强制执行平滑约束。估计在贝叶斯模型中进行，其中显式考虑了异常值以实现稳健性。VFC 算法及其变种（Ma 等人 2015b，2017a，2019b）已被证明是有效的。

4.5.4 宽松方法¶

最近的趋势是开发宽松方法进行匹配，其中几何约束被放松以适应复杂情况，例如由宽基线的图像对或具有独立运动的对象引起的运动不连续性。某些 GM 方法（Leordeanu 和 Hebert 2005；Liu 和 Yan 2010）可用于这种要求，使用包括对应关系的成对几何关系的二次模型，以找到潜在正确的几个。然而，结果通常较粗糙。

Lipman 等人（2014）考虑了分段仿射变形，然后将特征匹配形式化为一个受约束的优化问题，该问题寻找与大多数对应关系一致的变形，并施加了有界的畸变。Lin 等人（2014，2017）提出了在特定设计的对应域中使用非线性回归技术估计的似然函数来识别真实匹配项，在这个对应关系领域，施加了运动连贯性，同时也允许不连续性。这个概念对应于强制局部运动连贯性约束。Ma 等人（2018a，2019d）提出了一种用于匹配的保持局部性的方法，其中匹配的全局畸变模型被放松以专注于每个对应关系的局部性，以换取通用性和效率。所得到的标准已被证明能够迅速准确地过滤错误的匹配项。在 Bian 等人（2017）中出现了类似的方法，引入了一种基于局部支持匹配的简单标准，用于拒绝异常值。Jiang 等人（2020a）将特征匹配形式化为一种带有异常值的空间聚类问题，以自适应地将虚拟匹配项聚类到几个运动一致的簇中，同时还有一个异常值/误匹配簇。在 Lee 等人（2020）中，另一种方法将特征匹配问题形式化为马尔可夫随机场，使用局部描述符距离和相对几何相似性增强了鲁棒性和准确性。

4.6 基于学习的匹配¶

除了检测器或描述符，基于学习的匹配方法通常用于替代传统方法进行信息提取和表示或模型回归。通过学习进行的匹配步骤可以大致分类为基于图像和基于点的学习。基于传统方法，前者旨在处理三种典型任务，即图像配准（Wu 等，2015a），立体匹配（Poursaeed 等，2018）以及相机定位或变换估计（Poursaeed 等，2018；Erlik Nowruzi 等，2017；Yin 和 Shi，2018）。这种方法可以直接实现基于任务的学习，而不需要提前检测任何显著的图像结构（例如兴趣点）。相比之下，基于点的学习更喜欢在提取的点集上进行；这些方法通常用于点数据处理，如分类、分割（Qi 等，2017a, b）和配准（Simonovsky 等，2016；Liao 等，2017）。研究人员还使用这些方法来从候选匹配集中选择正确的匹配并估计几何变换模型（Moo Yi 等，2018；Ma 等，2019a；Zhao 等，2019；Ranftl 和 Koltun，2018）。

4.6.1 从图像学习¶

基于图像学习的匹配方法通常使用卷积神经网络（CNN）来进行图像级潜在信息提取、相似度测量以及几何关系估计。因此，基于图像区域的学习（第 3.3 节：基于学习的特征描述符）经常被用作面积基础的图像配准和立体匹配的扩展。这是因为滑动窗口中的传统相似性测量可以很容易地替换为深度方式，即深度描述符。然而，研究人员在使用深度学习进行空间变换网络（STN）（Jaderberg 等，2015）和光流估计（FlowNet）（Dosovitskiy 等，2015）方面取得的成功引发了一系列研究，直接使用深度学习技术来估计几何变换或非参数形变场，甚至实现端到端可训练的框架。

图像配准。对于基于区域的图像配准，早期的深度学习通常被用作传统配准框架的直接扩展，并且后来使用强化学习范式来迭代估计变换，甚至直接估计注册任务的变形场或位移场。最直观的方法是使用深度学习网络来估计目标图像对的相似度测量，以驱动迭代优化过程。通过这种方式，传统的测量指标，如相关性和 MI 方法等，可以用更优越的深度指标来替代。例如，Wu 等人（2015a）通过使用卷积堆叠自编码器（CAE）来实现可变形图像配准，以从观察到的图像块数据中发现紧凑且高度可区分的特征，用于相似性度量的学习。类似地，为了获得更好的相似性度量，Simonovsky 等人（2016）使用了从几个对齐的图像对中训练得到的深度网络。此外，一种称为 Quicksilver 的快速可变形图像配准方法（Yang 等，2017b）通过直接使用图像外观来预测大变形等距模型的补丁预测来实现。受到深度卷积的启发，Revaud 等人（2016）引入了一种基于分层相关架构的密集匹配算法。该方法可以处理复杂的非刚性变形和重复纹理区域。Arar 等人（2020）介绍了一种基于图像到图像翻译网络的无监督多模态图像配准技术，其中包含几何保持约束。

与度量学习不同，无监督配准使用了一个训练有素的代理来进行图像配准，通常用于估计刚性变换模型或可变形场。Liao 等人（2017）首次使用了强化学习进行刚性图像配准，其中使用了人工代理和与注意力驱动层次策略耦合的贪婪监督方法，以实现“策略学习”过程并找到产生图像对齐的最佳运动操作序列。在 Krebs 等人（2017）中，还训练了一个人工代理，通过从大量合成变形图像对中训练来探索统计变形模型的参数空间，以处理可变形注册问题和提取真实数据的可靠变形场的困难。与使用单一代理不同，Miao 等人（2018）提出了一种用于医学图像配准的多代理强化学习范式，其中自动关注机制用于接收多个图像区域。然而，强化学习通常用于预测回归过程的迭代更新，并且在迭代过程中仍然消耗大量计算。

为了减少运行时间并避免明确定义不相似度度量，研究越来越多地关注一次性端到端配准。Sokooti 等人（2017）首次设计了深度回归网络，直接从一对输入图像中学习位移向量场。另一种方法在 de Vos 等人（2017）中类似地训练了一个深度网络来回归和输出空间变换的参数，然后可以生成位移场以将移动图像变形到目标图像。然而，仍然需要图像对之间的相似性度量来实现无监督优化。最近，de Vos 等人（2019）引入了一个深度学习框架，用于无监督的仿射和可变形图像配准。训练好的网络可以用于一次性配准一对看不见的图像。将深度网络视为回归器的类似方法可以直接从图像对中学习参数变换模型，例如基础矩阵（Poursaeed 等，2018），单应矩阵（DeTone 等，2016）和非刚性变形（Rocco 等，2017）。

还出现了许多其他端到端图像级学习的注册方法。Chen 等人（2019）提出了端到端可训练的深度网络，用于直接预测用于图像对齐的密集位移场。Wang 和 Zhang（2020）介绍了用于高效可变形医学图像配准的 DeepFLASH，该方法在低维带宽有限空间中实现，从而显著减少了计算和内存需求。为了同时增强变换模型的拓扑保持性和平滑性，Mok 和 Chung（2020）提出了一种有效的无监督对称图像配准方法，该方法最大化了在不同态映射空间内的图像之间的相似性，并同时估计了正向和反向变换。在 Truong 等人（2020）中，作者介绍了一种用于几何匹配、光流估计和语义对应的通用网络，通过研究全局和局部相关层的联合使用，可以实现高准确性和稳健性。有关配准的具体评论请参阅（Ferrante 和 Paragios，2017；Haskins 等，2020）。

立体匹配。在过去的几年中，与配准类似，立体匹配的众多研究重点是通过使用深度卷积技术准确计算匹配代价并优化视差图（Zbontar 和 LeCun，2015；Luo 等，2016；Zbontar 和 LeCun，2016；Shaked 和 Wolf，2017）。除了深度描述符，如 DeepCompare（Zagoruyko 和 Komodakis，2015）和 MatchNet（Han 等，2015）等，Zbontar 和 LeCun（2015）引入了深度连体网络来计算匹配代价，这些网络经过训练可以预测图像块之间的相似性。他们进一步提出了一系列 CNNs（Zbontar 和 LeCun，2016）用于成对匹配的二进制分类，并将其应用于视差估计。与将匹配代价的计算转化为多标签分类问题类似，Luo 等人（2016）提出了一种用于快速立体匹配的高效连体网络。此外，Shaked 和 Wolf（2017）通过使用提议的常数高速公路网络计算匹配代价，以及用于反射性置信度学习的视差估计，提高了性能。

最近几年，这个匹配任务的端到端深度方式引起了越来越多的关注。例如，Mayer 等人（2016）在他们的 DispNet 中训练了一个端到端 CNN，以获得精细的视差图，该图通过 Pang 等人（2017）的两阶段 CNN（级联残差学习，CRL）进行扩展。更近期，Chang 和 Chen（2018）引入了一个空间金字塔池化模块以及三维卷积策略。这种方法可以利用全局上下文信息来增强立体匹配。受 CycleGAN（Zhu 等，2017）的启发，并为了处理域差异，Liu 等人（2020）提出了一个端到端训练框架，可以同时将所有合成立体图像转化为逼真图像，同时保持极线约束。这种方法是通过域翻译和立体匹配之间的联合优化来实现的。Yang 等人（2020）中的另一种方法学习了视差的小波系数而不是视差本身，可以从低频子模块学习全局上下文信息并从其他子模块学习细节。此外，还使用了引导策略（Zhang 等，2019a；Poggi 等，2019）进行立体匹配。

深度卷积技术在公共基准测试中的最佳性能主导了它们在立体匹配领域的应用。然而，CNN 在立体匹配领域的应用受到输入图像对的限制，这些图像通常是从具有狭窄基线和极线校正的双目摄像机中捕获的。然而，这些基于学习的立体匹配中的网络结构、基本思想以及一些技巧或策略对于一般图像匹配任务可能具有很强的参考价值。

4.6.2 从点学习¶

从点学习不如图像学习受欢迎，用于特征提取、表示和相似性测量。基于点的学习，特别是用于特征匹配，仅在近年来被引入。这是因为在点数据上使用 CNN 比在原始图像上更加困难，因为点的无序结构和稀疏点的分散性质。此外，使用深度卷积技术来操作和提取多点之间的空间关系，如相邻元素、相对位置、长度和角度信息等，是具有挑战性的。然而，使用深度学习技术解决基于点的任务已经引起了越来越多的关注。这些技术可以大致分为参数拟合（Brachmann 等，2017；Ranftl 和 Koltun，2018）和点分类和/或分割（Qi 等，2017a, b；Moo Yi 等，2018；Ma 等，2019a；Zhao 等，2019）。前者受到经典的 RANSAC 算法的启发，旨在通过使用 CNN 进行数据驱动的优化策略来估计变换模型，例如基础矩阵（Ranftl 和 Koltun，2018）和极点几何（Brachmann 和 Rother，2019）。然而，后者倾向于训练分类器来从候选匹配集中识别真实的匹配项。通常，参数拟合和点分类通常联合训练以提高性能。

对于可训练的基础矩阵估计，Brachmann 等人（2017）提出了一种可微分的 RANSAC，称为 DSAC，它是基于端到端的强化学习的。他们通过概率选择取代了确定性假设选择，以减小期望损失并优化可学习的参数。随后，Ranftl 和 Koltun（2018）提出了一种用于从噪声中估计基础矩阵的可训练方法，将其建模为一系列加权齐次最小二乘问题，其中使用深度网络估计了鲁棒权重。与 DSAC 类似，Brachmann 和 Rother（2019）以及 Kluger 等人（2020）也引入了使用学习技术来改进重采样策略的方法。Brachmann 和 Rother（2019）提出了 NG-RANSAC，这是一种使用假设采样的学习引导的鲁棒估计器。它将内点数本身作为训练目标，以促进 NG-RANSAC 的自监督学习，并可以合并非可微分的任务损失函数和非可微分的最小求解器。而 CONSAC（Kluger 等人，2020）被引入作为多参数模型拟合的鲁棒估计器。它使用神经网络来顺序更新假设选择的条件采样概率。

近年来，已经开发了基于学习的误匹配移除方法。Moo Yi 等人（2018）首次尝试引入一种称为“学习寻找好对应”的学习技术（LFGC），旨在从一组稀疏的假定匹配以及刚性几何变换约束下的图像内参中训练网络，然后将测试的对应关系标记为内点或外点并同时输出相机运动。然而，LFGC 可能会牺牲许多真正的对应关系来估计运动参数，无法处理一般的匹配问题，如可变形和非刚性图像匹配。为此，Ma 等人（2019a）提出了一个用于误匹配移除的通用框架，称为 LMR，它使用了少量图像和手工几何表示进行训练。他们的方法在线性时间复杂度下显示出了有希望的匹配性能。最近，Zhang 等人（2019b）专注于基于其 order-aware 网络（OAN）的几何恢复，并在姿态估计方面取得了有希望的性能。Sarlin 等人（2020）提出了 SuperGlue，通过联合查找对应关系和拒绝不可匹配的点，将两组局部特征进行匹配。这种方法使用图神经网络（Scarselli 等人，2009）来实现可微传输问题的优化。类似的图神经网络流水线已经被采用，其中包括深度图匹配（Wang 等人，2019；Yuetal.2020a；Fey 等人，2020）等新兴研究分支，其中提出并采用了跨图卷积（Wang 等人，2019）、通道独立嵌入（Yu 等人，2020a）和基于样条的卷积（Fey 等人，2020）用于监督图匹配学习。

尽管将 CNN 应用于点数据是困难的，但最新的技术显示出在矩阵估计和点数据分类方面具有巨大潜力，特别是对于具有挑战性的数据或场景。此外，自然语言处理中的多层感知方法和图卷积技术也可以作为处理匹配任务中这些分散和非结构化的点数据的有力参考。

4.7 三维情况下的匹配¶

与其二维对应物类似，三维匹配方法通常包括两个步骤，即关键点检测和局部特征描述，然后可以通过计算描述符之间的相似性来建立稀疏对应关系集。尽管大多数方法使用局部特征描述符来建立 3D 实例之间的对应关系，这些描述符设计为对噪声和变形具有鲁棒性，以建立 3D 实例之间的对应关系，但有各种经典和最近的工作属于另一类。考虑到文献综述超出了本文的范围，我们将读者转至最近的调查（Biasotti 等人，2016；Van Kaick 等人，2011），因为这些调查对形状匹配领域的文献进行了详细的回顾。

嵌入方法的目标是通过利用一些自然假设（例如，近似等距性）来减少可跟踪性的自由度，以更简单的方式参数化复杂的匹配问题。Elad 和 Kimmel（2003）提出了一种传统方法，通过在中间欧几里得空间中嵌入形状来匹配形状。在这种方法中，测地距离被近似为欧几里得距离，原始的非刚性配准问题在中间空间中被降低到刚性配准问题。值得注意的是，另一项工作开发了使用嵌入空间的共形映射方法（Lipman 和 Funkhouser，2009；Kim 等人，2011；Zeng 等人，2010）。

更直接的方法是通过最小化结构失真来在形状上点对点匹配（子集），这个公式由 Bronstein 等人（2006）开发，他们引入了一个高度非凸且不可微的目标，以及用于优化的广义多维尺度技术。一些研究人员还尝试减轻计算复杂性高的问题（Sahillioglu 和 Yemez，2011；Tevsetal.2011），同时考虑图匹配中的二次分配公式（Rodola 等人，2012，2013；Chen 和 Koltun，2015；Wang 等人，2011）。

基于功能图框架的方法家族首先由 Ovsjanikov 等人（2012）开发。这些方法不是在欧几里得空间中进行点对点匹配，而是使用两个流形之间的功能图来表示对应关系，这可以由线性算子来表征。通过使用 Laplace-Beltrami 算子的特征基，功能图可以以紧凑的形式编码。在这种公式中，大多数关于映射的自然约束，如地标对应和算子可交换性，在这个公式中都变成了线性的，从而实现了高效的解决方案。这种方法被采用并扩展到许多后续工作中（Aflalo 等人，2016；Kovnatsky 等人，2015；Pokrass 等人，2013；Rodolà等人，2017；Litany 等人，2017）。

在三维情况下的点集学习也是一个热门话题。Yew 等人（2020）提出了用于刚性点云配准的 RPM-Net，它通过学习融合特征来减小初始化并提高收敛性能。Gojcic 等人（2020）引入了一种端到端的多视点点云配准框架，直接学习以一种全局一致的方式注册场景的所有视图。Pais 等人（2020）引入了一种用于 3D 点云配准的学习架构，称为 3DRegNet。这种方法可以从一组假定匹配中识别出真实的点对应关系，并回归运动参数以将扫描对齐到共同的参考框架。Choy 等人（2020）使用高维卷积网络来检测高维空间中的线性子空间，然后将其应用于刚性运动和图像对应估计的 3D 配准。

4.8 总结¶

给定一对相似对象/场景的图像，无论是否进行了特征检测和/或描述，匹配任务都已扩展到了几种不同的形式，例如图像配准、立体匹配、特征匹配、图匹配和点集配准。这些不同的匹配定义通常是为了特定应用而引入的，各自具有其优势。

传统的图像配准和立体匹配通过使用基于块的相似性测量和优化策略来实现密集匹配，以搜索全局最优解。但是，它们是在具有高重叠区域（轻微几何变形）和双目摄像机的图像对上进行的，这可能需要大量的计算负担和有限的手工制作测量指标。

深度学习的引入由于网络设计和损失定义的进步以及丰富的训练样本，提高了配准精度和视差估计。然而，我们还发现，将深度学习应用于这些匹配任务通常是在经历轻微几何变形的图像对上进行的，例如医学图像配准和双目立体匹配。将它们应用于更复杂的场景，如宽基线图像立体匹配或具有严重几何变形的图像配准，仍然是一个开放的问题。

基于特征的匹配可以有效解决大视角、宽基线和严重非刚性图像匹配问题中的限制。在文献中提出的方法中，最流行的策略是基于描述符距离构建假定匹配，然后使用鲁棒估计器（如 RANSAC）。然而，在假定匹配集中存在大量误匹配可能会对后续视觉任务的性能产生负面影响，并且需要相当长的时间来估计模型。因此，需要误匹配移除方法，并将其集成到具有额外几何约束的情况下，以尽可能保留尽可能多的真实匹配，并将误匹配保持在最低水平。具体来说，基于重采样的方法，如 RANSAC，可以估计潜在参数模型并同时去除离群值。然而，它们在需要处理更复杂的非刚性变换的图像对时，其理论上所需的运行时间随着离群值比率的增加而呈指数增长。非参数模型的方法可以通过使用高维非参数模型来处理非刚性图像匹配问题，但在更复杂的解决方案空间中定义目标函数和找到最优解仍然具有挑战性。与重采样和非参数模型方法中的全局约束不同，松弛的误匹配移除方法通常是在潜在内点的局部连贯假设的基础上进行的。因此，设计了更简单但高效的规则来过滤离群值，同时在极短的时间内保留内点。但是，这类方法由于参数敏感性而受到限制；此外，它们容易保留明显的离群值，从而影响了后续姿态估计和图像配准的精度。

此外，基于图像块描述符的方法可能因要求在纹理较少的图像、形状、语义图像和直接从特定设备捕获的原始点时，而无法工作。因此，对于执行这些情况的匹配任务，图匹配和点配准方法更加合适。邻域点之间的图结构和整体对应矩阵被应用于优化和找到最优解。然而，这些纯粹基于点的方法受限于计算负担和离群值敏感性的限制。因此，在图像匹配领域中设计适当的问题公式和约束条件，并提出更高效的优化方法，仍然是一个开放的问题，并需要进一步的研究关注。

类似于基于图像的学习，越来越多的研究在基于特征的匹配领域中使用深度学习。最新的技术已经显示出在矩阵估计（例如基础矩阵）和点数据分类（例如误匹配移除）方面，使用深度回归器和分类器具有巨大的潜力，特别是用于处理具有挑战性的数据或场景。然而，由于这些稀疏点的无序结构和分散性质，将卷积网络应用于点数据并不像在原始图像上那样容易。然而，最近的研究表明，在这种点数据上使用图卷积策略和多层感知方法，以及对这种点数据进行特定规范化，是可行的。除了刚性变换参数估计之外，使用深度卷积技术在点数据上进行非刚性甚至严重变形的匹配可能是一个更具挑战性和重要的问题。

5 基于匹配的应用¶

图像匹配是计算机视觉中的一个基本问题，并被认为是许多不同应用的关键前提。在本节中，我们简要回顾了几个代表性的应用。

5.1 SfM¶

运动恢复（Structure-from-Motion，SfM）涉及从一系列图像中恢复静止场景的三维结构，这些图像是从不同视点获得的，通过估计与这些图像对应的相机运动来获得。SfM 包括三个主要阶段，即（i）跨图像的特征匹配，（ii）相机姿态估计，以及（iii）使用估计的运动和特征恢复三维结构。其有效性在很大程度上取决于可接受的特征匹配集。

在现代 SfM 系统中（Schonberger 和 Frahm 2016；Wu 2018；Sweeney 等人 2015），特征匹配管道广泛应用于图像，即特征检测、描述和最近邻匹配，以提供初始对应关系。初始对应关系包含大量的离群值。因此，需要几何验证，通过使用 RANSAC（Fischler 和 Bolles 1981）来估计基础矩阵来解决。这可以通过误匹配移除方法来解决。

同时，为了增强 SfM 任务，研究人员已经专注于进行稳健的特征匹配，即建立丰富准确的对应关系。显然，高级描述符可以极大地影响这个任务（Fan 等人 2019）。此外，Shah 等人（2015）提出了一种几何感知方法，最初使用少量特征来估计图像之间的极线几何，并利用它来引导匹配其余特征。Lin 等人（2016b）利用 RANSAC 来引导不同真伪匹配的匹配一致性曲线的训练。他们的方法追踪了在重建现代城市的宽基线和重复结构方面的常见问题。这些对应关系也是相机姿态估计的前提条件，已经研究了用于此任务的常用 RANSAC 的有效替代方法（Moo Yi 等人 2018），具有识别良好对应关系的预阶段。

5.2 SLAM¶

获取环境地图是自主移动机器人的基本任务，因此形成了许多不同的高级任务的基础，例如导航和定位。同时定位与建图（SLAM）问题（Davison 等人 2007；Mur-Artal 等人 2015；Sturm 等人 2012）在几十年来受到了密切关注。

在常见的 SLAM 系统中，需要特征匹配来建立帧之间的对应关系，然后作为估计相对相机姿态和定位的输入。与 SfM 类似，大多数 SLAM 系统中使用了完整的特征匹配管道。通常，在 Endres 等人（2012）的工作中，引入了特征匹配以在前端从传感器数据中建立空间关系。已知的 SIFT（Lowe 2004）、SURF（Bay 等人 2008）和 ORB（Rublee 等人 2011）算法可选用于检测和描述特征，然后使用 RANSAC（Fischler 和 Bolles 1981）进行稳健匹配。

关于不同特征检测器和描述符的评估可以在 Gil 等人（2010）中找到。最近，Lowry 和 Andreasson（2018）提出了一种用于视觉定位的空间验证方法，该方法在存在大量离群值的情况下具有稳健性。对于一个感知 3D 范围扫描的 SLAM 系统，点集配准方法（例如 ICP）（Nüchter 等人 2007）也用于扫描匹配和定位机器人。

回环检测是 SLAM 应用中的另一个核心模块，它指的是准确确定机器人是否已返回以前访问过的位置。这对于减少由累积误差引起的轨迹漂移至关重要。已经开发了一组基于外观的方法，使用图像相似性来识别以前访问过的位置。特征匹配结果自然适用于测量两个场景的相似性，并且已经成为许多最先进方法的基础。例如，Liu 和 Zhang（2012）在当前图像与每个以前访问的图像之间执行 SIFT 的特征匹配，然后基于结果中准确匹配的数量确定了闭环。Zhang 等人（2011）使用了从图像中提取的原始特征的定向匹配来检测闭环事件。为了实现闭环检测，Wu 等人（2014）使用 LSH 作为基本技术，通过将当前视图中的二进制视觉特征与机器人外观地图中的视觉特征进行匹配来进行匹配。Liu 等人（2015a）开发了一种一致性约束以剪枝离群值，并验证了他们的方法在闭环检测方面的优越性。

5.3 视觉导航¶

视觉导航旨在基于视觉信息将机器人从任意起始位置导航到目标或回家位置。通常，特征匹配用作视觉导航研究中对应方法的构建块（Möller 等人 2010）。在这个类别中，导航矢量可以通过将对应关系转化为运动流来确定（Ma 等人 2018b；Churchill 和 Vardy 2013；Liu 等人 2013；Zhao 和 Ma 2017）。

Ramisa 等人（2011）结合了在全景图像中自动检测到的平均地标矢量和不变特征点来实现自主视觉导航。然而，该方法中的特征匹配仅由描述符的相似性确定，从而导致了一些误匹配的问题。已验证离群值的存在是导致视觉导航性能下降的原因（Schroeter 和 Newman 2008）。为了解决由误匹配引起的性能下降，Liu 等人（2013）使用了类似 RANSAC 的方法来消除误匹配。与此同时，Zhao 和 Ma（2017）提出了一种视觉导航方法，同时进行误匹配移除和在平滑性先验下稀疏运动流的稳健插值。Ma 等人（2018b）还提出了一种引导的局部保持匹配方法，以处理极大比例的离群值并提高视觉导航的稳健性。

5.4 图像配准和拼接¶

图像配准是将来自不同视点、不同时刻或不同传感器获得的同一场景的两个或多个图像对齐的过程（Zitova 和 Flusser 2003）。在过去几十年中，基于特征的方法，其中关键要求是特征匹配，因其稳健性和效率而引起了越来越多的关注。一旦建立了对应关系，图像配准就被简化为估计变换模型（例如刚性、仿射或投影）。最后，源图像通过映射函数进行变换，该函数依赖于某种插值技术（例如双线性和最近邻）。已经提出了大量用于特征匹配和图像配准的方法。Ma 等人（2015b）提出了刚性和非刚性特征匹配和图像配准的贝叶斯公式。为了进一步利用几何线索，局部线性变换约束被并入。他们还最近提出了一个引导的局部保持匹配方法（Ma 等人 2018a）。他们提出的方法可以显著减少计算复杂性，并能够处理更复杂的变换模型。对于非刚性图像配准问题，Pilet 等人（2008）和 Gay-Bellile 等人（2008）提出了解决方案，其中稳健的匹配技术不受离群值的影响。一些工作（Paul 和 Pati 2016；Ma 等人 2017b；Yang 等人 2017a）还尝试修改特征检测器和描述符以改进配准过程。

多模态图像配准问题更加复杂，因为不同模态引起的外观高度变化，这在医学图像和多传感器图像分析中经常出现。例如，Chen 等人（2010）开发了部分强度不变特征描述符（PIIFD）以注册视网膜图像，而 Wang 等人（2015）在 SURF 检测器（Bay 等人 2008）和单一高斯点匹配模型的更稳健注册框架中扩展了 PIIFD。基于多模态图像的特点，Liu 等人（2018a）提出了一种基于尺度不变 PIIFD 特征和局部保持匹配的红外和可见图像注册描述符。Du 等人（2018）还提出了一种基于尺度不变 PIIFD 特征和局部保持匹配的红外和可见图像注册方法。Ye 等人（2017）提出了一种基于图像结构特性的多模态注册的新型特征描述符。关于医学图像分析领域基于特征匹配的多模态注册技术的详细讨论，它们被分类为几何方法，可以在 Sotiras 等人（2013）中找到。

与图像配准相比，图像拼接或图像镶嵌涉及从部分视图的序列中获取更广阔的场景视野（Ghosh 和 Kaabouch 2016）。与图像配准相比，图像拼接处理重叠度较低的图像，并要求在像素级别进行准确对齐，以避免视觉不连续性。由于其不变性属性和效率，基于特征的拼接方法在这个领域很受欢迎。例如，为了识别几何上一致的特征匹配并实现准确的单应性估计，Brown 和 Lowe（2007）提出了使用 SIFT（Lowe 2004）特征匹配和 RANSAC（Fischler 和 Bolles 1981）算法。Lin 等人（2011）使用 SIFT（Lowe 2004）来预先计算匹配，然后联合估计匹配和光滑变化的仿射场，以获得更好的拼接性能。感兴趣的读者可以参考综合调查（Ghosh 和 Kaabouch 2016；Bonny 和 Uddin 2016）以获取更多基于特征的图像镶嵌和拼接方法的概述。

5.5 图像融合¶

为了生成更有利于后续应用的图像，图像融合用于将不同传感器或不同拍摄设置下获取的图像中的有意义信息进行组合（Pohl 和 Van Genderen 1998），其中源图像已经精确对齐。图像融合的前提是使用特征匹配方法对源图像进行注册，而注册的准确性直接影响融合质量。Liu 等人（2017）使用 CNN 来共同生成多焦点图像融合的活动水平测量和融合规则。同时，Ma 等人（2019c）提出了一种红外和可见图像融合的端到端模型，该模型在生成对比度突出的红外强度和基于生成对抗网络的可见梯度的图像下工作。随后，他们引入了细节损失和目标边缘增强损失以进一步丰富纹理细节（Ma 等人 2020）。

一组方法旨在基于局部特征融合图像，其中密集 SIFT 是最受欢迎的。Liu 等人（2015b）提出了多焦点图像的密集尺度不变特征变换融合，其中局部特征描述符不仅用作活动水平测量，还用于匹配多个源图像之间的未对齐像素以改善融合结果的质量。同样，Hayat 和 Imran（2019）提出了一种使用密集 SIFT 描述符和引导滤波器的无幽灵多曝光图像融合技术，可使用普通相机生成高质量图像。此外，Chen 等人（2015）和 Ma 等人（2016a）提出了一种可以同时进行图像配准和图像融合的方法，从而在不对齐的图像对上实现图像融合。

5.6 图像检索、物体识别和跟踪¶

特征匹配可用于衡量图像之间的相似性，从而使一系列高级应用成为可能，包括图像检索（Zhou 等人 2017）、物体识别和跟踪。图像检索的目标是检索出对于给定查询图像展现相似场景的所有图像。在基于局部特征的图像检索中，图像相似性本质上是由图像之间的特征匹配决定的。因此，可以通过聚合来自匹配特征的投票来获得图像相似性得分。在 Zhou 等人（2011）的工作中，相关性分数仅由两个图像之间的特征匹配数量确定。在 Jégou 等人（2010）中，评分函数定义为共享视觉单词上的平方项频率逆文档频率权重的累加，这本质上是内部产品特征的一个特征包。

此外，几何上下文验证是一种常见的用于改进初始图像检索结果的技术，它与特征匹配直接相关。通过融入几何信息，几何上下文验证技术可用于解决由于局部描述符的模糊性和量化损失导致的误匹配问题。对于图像检索，许多方法采用显式方法来估计变换模型以验证暂时的匹配。例如，Philbin 等人（2007 年）使用了一种类似于 RANSAC 的方法来查找内点对应关系，而 Avrithis 和 Tolias（2014 年）则开发了一个受霍夫变换空间中投票启发的简单的空间匹配模型。另一种方法处理几何上下文验证，而不明确处理变换模型。例如，Sivic 和 Zisserman（2003 年）利用局部特征组中的空间上下文的一致性来验证临时的对应关系。Zhou 等人（2010 年）提出了空间编码方法，通过验证全局相对位置的一致性来识别有效的视觉词匹配。

作为用于测量相似度的功能，特征匹配在目标识别和跟踪中也发挥着重要作用。例如，Lowe 等人（1999 年）使用 SIFT 特征来匹配示例图像和新图像。在他们提出的方法中，通过 Hough 变换哈希表来识别潜在的模型姿态，然后通过最小二乘拟合来得出模型参数的最终估计。如果至少有三个关键点在模型参数上达成一致，且残差较低，则物体的存在明显可见。现代的目标识别尝试还包括一些特定的手工制作特征（Dalal 和 Triggs 2005；Hinterstoisser 等人 2012）以及更近期的深度学习方法（Wohlhart 和 Lepetit 2015）。

跟踪基本上是指估计物体在图像上的轨迹。跨图像的特征匹配是基于特征的跟踪的基础，文献中已经提出了各种用于这些任务的算法。在大多数视觉跟踪系统中采用了特征匹配流程，只是匹配被限制在已知特征的那些被预测在接触位置附近的特征上。读者可以参考 Gauglitz 等人（2011 年）对用于跟踪的不同特征检测器和描述符的全面评估，以及最近提出的基准（Wu 等人 2015b），该基准涵盖了现代物体跟踪方法的回顾以及特征表示方法的作用。

思维导图¶

大纲形式